I would say that SPM math is a pretty poor indicator of how good your math skills are, as it promotes rote memorization instead of understanding. Good unis will probably try to let you understand concepts. Like my first year in uni, it completely blew my mind on how mathematics really was.
Engineering Simple Guide to Engineering, Read here first before posting new topic


 Mar 25 2014, 05:23 PM
Mar 25 2014, 05:23 PM
 Quote
Quote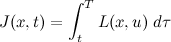
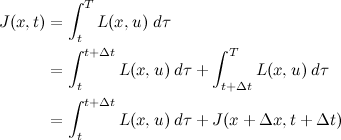
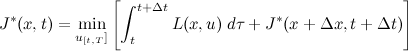
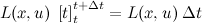 , and the second term, J*(x+Δx, t+Δt) can be approximated by its
, and the second term, J*(x+Δx, t+Δt) can be approximated by its 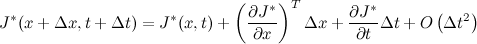
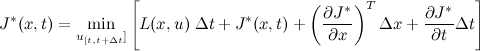
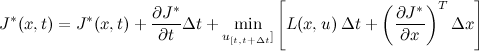
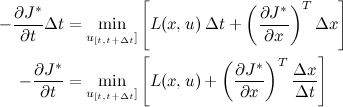
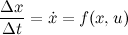 . Therefore, we obtain the following
. Therefore, we obtain the following 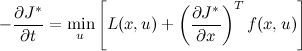

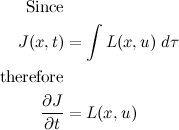

 0.0322sec
0.0322sec
 0.58
0.58
 6 queries
6 queries
 GZIP Disabled
GZIP Disabled