http://onsolver.com/
Original First Post
» Click to show Spoiler - click again to hide... «
College Algebra
» Click to show Spoiler - click again to hide... «
Calculus :: Early Transcendentals
» Click to show Spoiler - click again to hide... «
Advanced Engineering Mathematics
» Click to show Spoiler - click again to hide... «
Numerical Methods (a.k.a. Computational Methods for Applied Sciences)
» Click to show Spoiler - click again to hide... «
Euler Angles
» Click to show Spoiler - click again to hide... «
Operators & Symbols ::
(–x, y) ± + − × ÷ √ ² ³ ^ ∫ Σ Δ ∇ ∂ ∠ ° Ω “” → ← ↑ ↓ ∵ ∴ ½ ∞ ≈ ≠ ≪ ≤ ≥ ≫ • · ∝ † ⊗ ✔ ✘ 2⁄2 x≈-1.25992 ∧ ‖a‖ y≈-1.5874 …
Common Greek alphabets in Rotational dynamics:
ϕ, θ, ψ, ω
PID Controller ::
u = − (Ki*∫ x + Kp*x + Kd*ẋ)
| 15° | π/12 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 75° | 5π/12 |
| 90° | π/2 |
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
b² – 4ac
Superscripts and subscripts ::
x⁰ x¹ x² x³ x⁴ x⁵ x⁶ x⁷ x⁸ x⁹ x⁺ x⁻ x⁼ x⁽ ⁾ xⁿ x* x˙ xˣ
x₀ x₁ x₂ x₃ x₄ x₅ x₆ x₇ x₈ x₉ x₊ x₋ x₌ x₍ ₎ xᵢ xᵣ xₑ xₙ
Greek alphabets (lowercase) ::
α, β, γ, δ, ε, ζ, η, θ, κ, λ, μ, ξ, π, ρ, σ, τ, υ, ϕ, φ, χ, ψ, ω
Greek alphabets (uppercase & lowercase) ::
| Αα Alpha | Νν Nu |
| Ββ Beta | Ξξ Xi |
| Γγ Gamma | Οο Omicron |
| Δδ Delta | Ππ Pi |
| Εε Epsilon | Ρρ Rho |
| Ζζ Zeta | Σσς Sigma |
| Ηη Eta | Ττ Tau |
| Θθ Theta | Υυ Upsilon |
| Ιι Iota | Φϕφ Phi |
| Κκ Kappa | Χχ Chi |
| Λλ Lambda | Ψψ Psi |
| Μμ Mu | Ωω Omega |
» Click to show Spoiler - click again to hide... «
[attachmentid=4328645]
This post has been edited by Critical_Fallacy: Apr 29 2023, 03:50 PM


 Aug 6 2013, 07:47 PM, updated 3y ago
Aug 6 2013, 07:47 PM, updated 3y ago

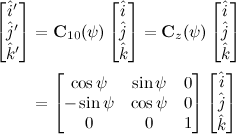
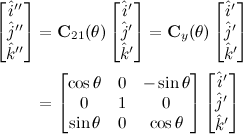
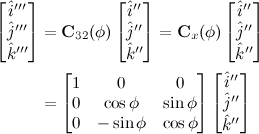

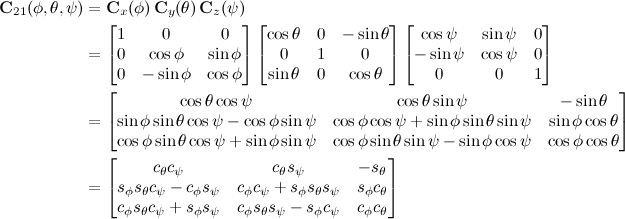

 Quote
Quote



 --->
---> 


 [/URL][/IMG]
[/URL][/IMG]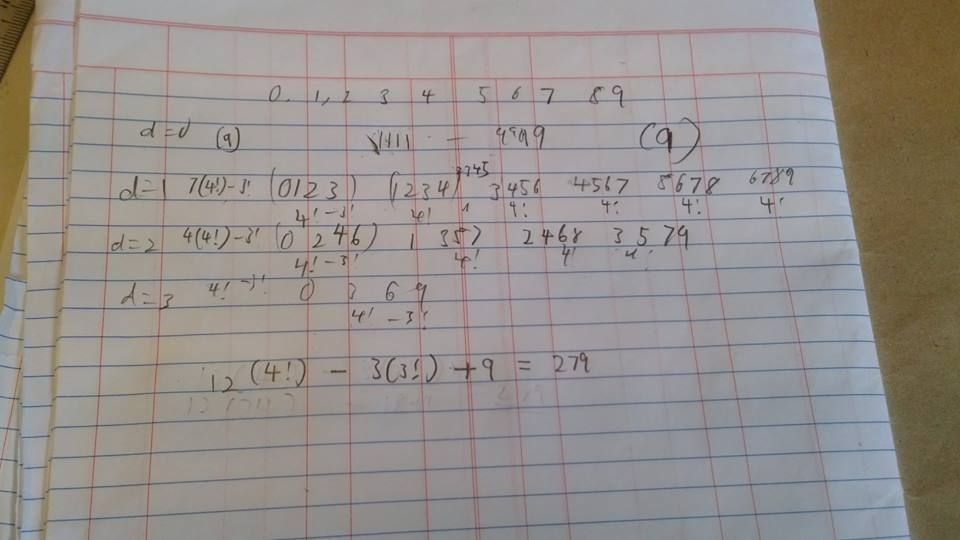 [/URL][/IMG]
[/URL][/IMG]



































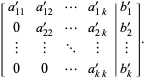














































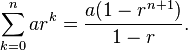


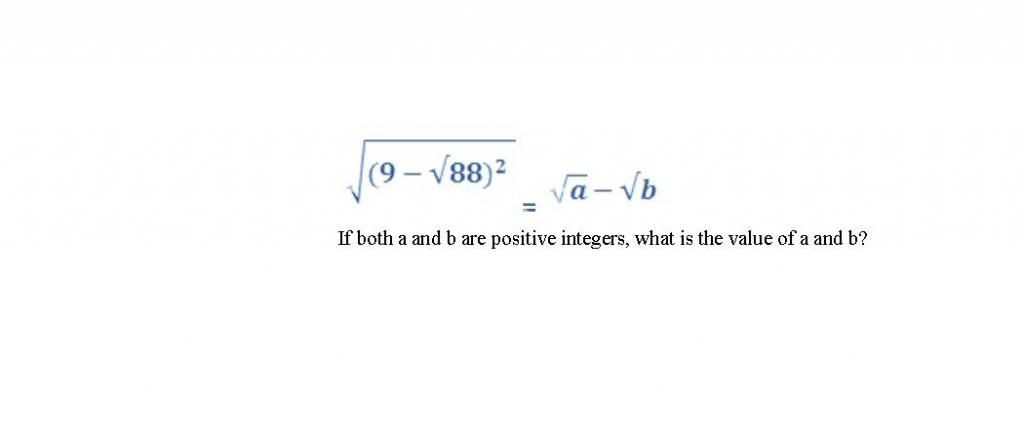












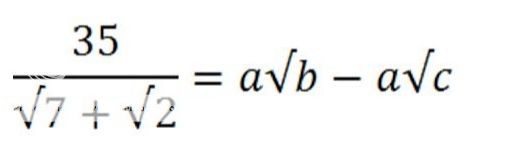
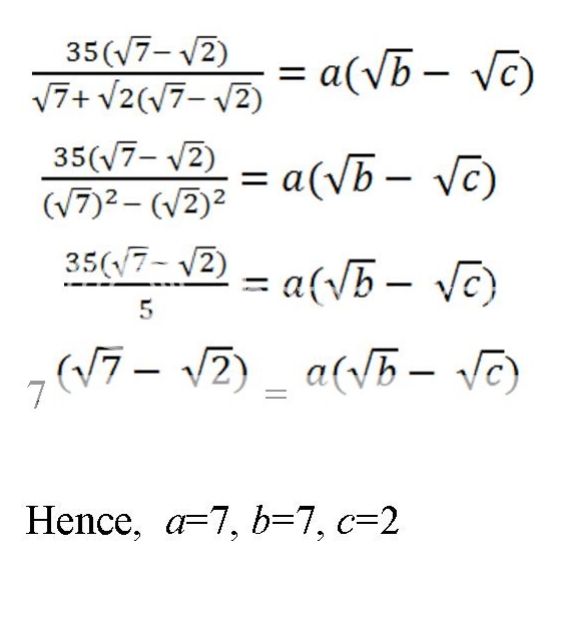



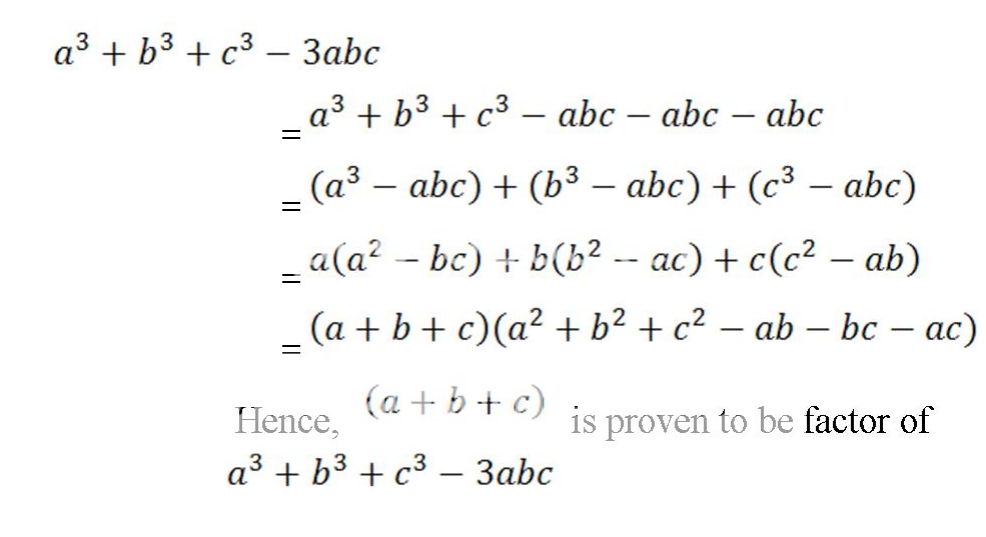























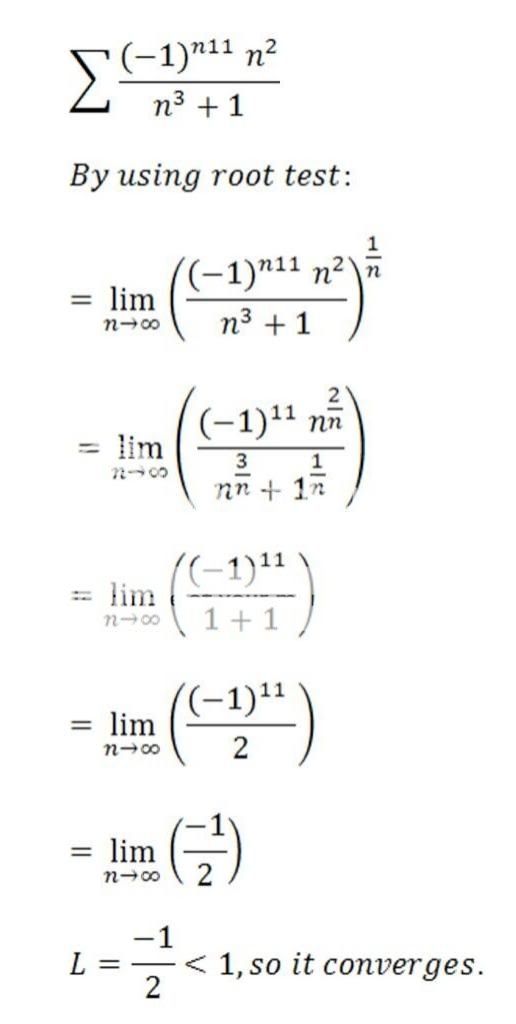

















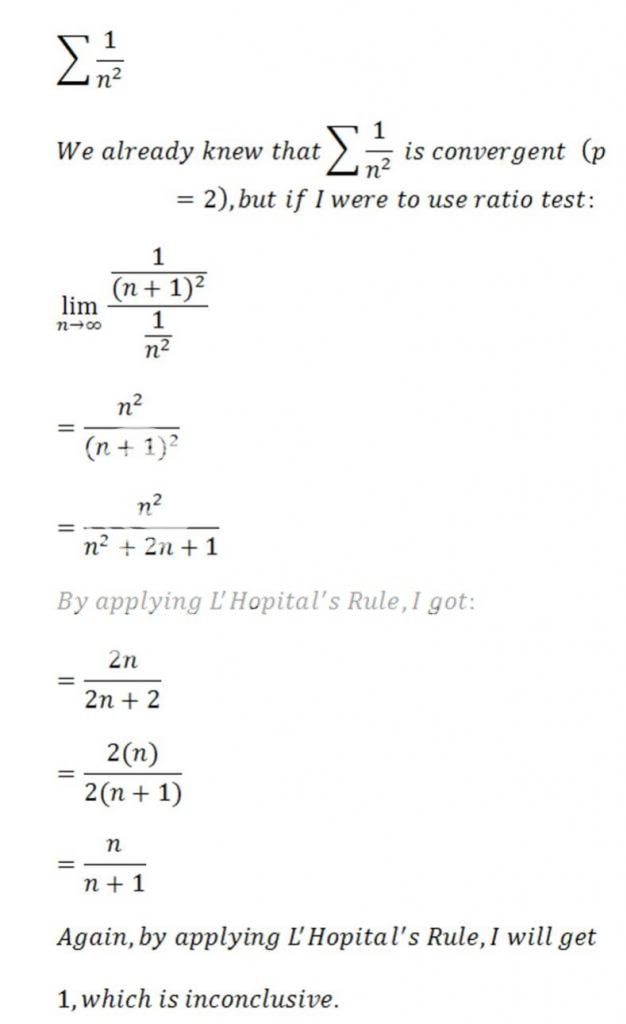
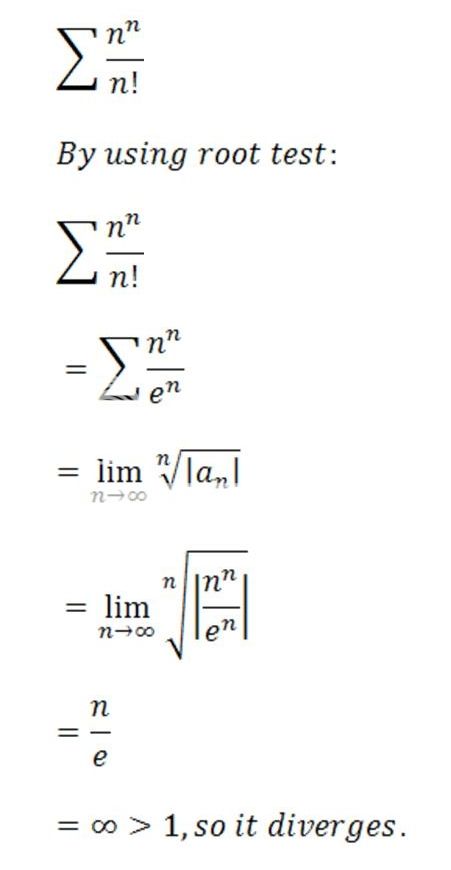






 .
. is rational or irrational. Thus, we have two cases here.
is rational or irrational. Thus, we have two cases here. and raise it to the power of
and raise it to the power of  , so that
, so that  , that is obviously rational, which in turn proves the theorem is correct.
, that is obviously rational, which in turn proves the theorem is correct. .
. .
. , because when
, because when  ,
,  ,
,  , it follows that
, it follows that  .
.
 .
. 


 , Sum Rule
, Sum Rule 
 , Product Rule
, Product Rule 


 and
and 




 and
and  , Logarithmic Differentiation
, Logarithmic Differentiation



 by using the elementary row operation (ERO)?
by using the elementary row operation (ERO)?  , only a maximum of seven (ERO) operations are required to get
, only a maximum of seven (ERO) operations are required to get  . In fact, ERO is nothing simpler than the basic arithmetic operations + − × ÷. By the way, ERO is NOT a formula,
. In fact, ERO is nothing simpler than the basic arithmetic operations + − × ÷. By the way, ERO is NOT a formula, 
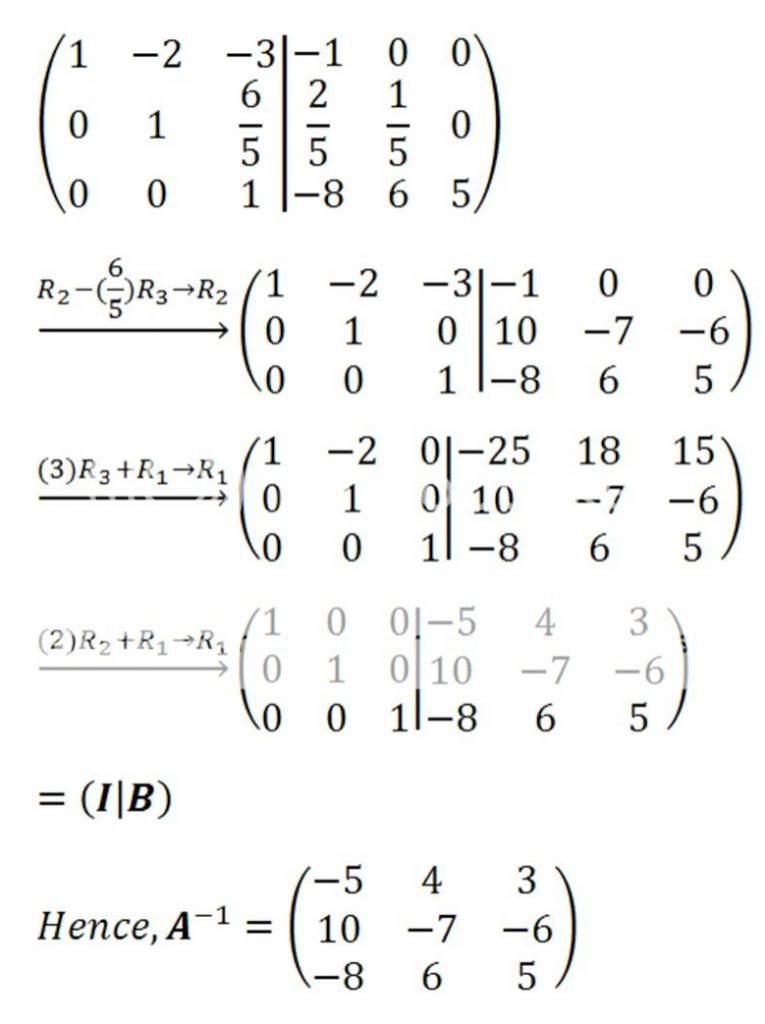




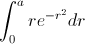
 .
. has no antiderivative, when you separate them by parts. The good news is that there is an easy way, called "
has no antiderivative, when you separate them by parts. The good news is that there is an easy way, called "





 of a curve is to exploit the slope formula of a straight line.
of a curve is to exploit the slope formula of a straight line. , and the upper bound
, and the upper bound  .
. and
and  , a straight line
, a straight line  can be drawn, where it intercepts x-axis. The x value that intercepts x-axis is closer to the real root,
can be drawn, where it intercepts x-axis. The x value that intercepts x-axis is closer to the real root, 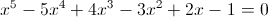 , and I guess it can't be solved, or perhaps I wasn't able to write down the root. I guess this has something to do with the Galois Theory, due to the fact that it's a quintic function. However, I can approximate the root by using Newton-Raphson method at least of it. Here it is:
, and I guess it can't be solved, or perhaps I wasn't able to write down the root. I guess this has something to do with the Galois Theory, due to the fact that it's a quintic function. However, I can approximate the root by using Newton-Raphson method at least of it. Here it is: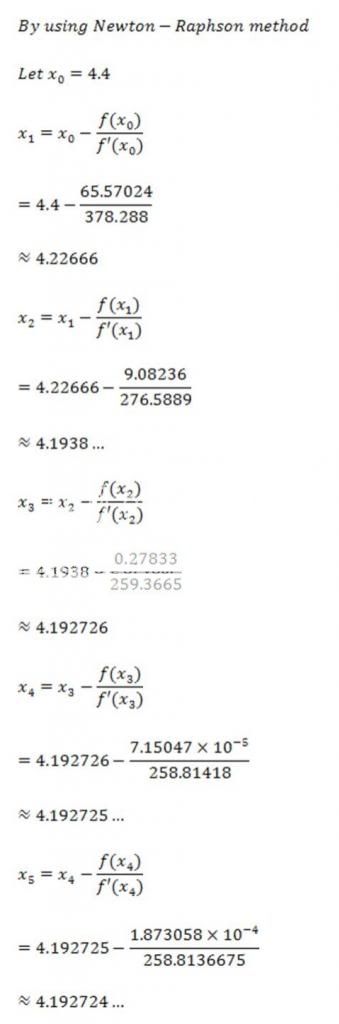




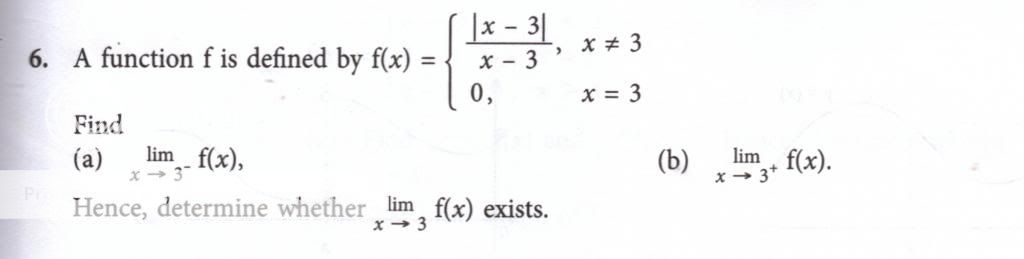



 approaches a different number from the right side of 3 than it approaches from the left side, the limit
approaches a different number from the right side of 3 than it approaches from the left side, the limit 
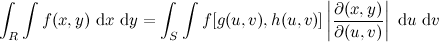
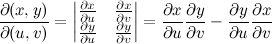
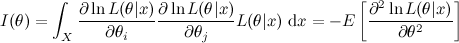
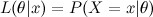
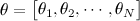 , the Fisher information takes the form of an N×N matrix as shown below.
, the Fisher information takes the form of an N×N matrix as shown below. 
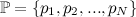 be the family of univariate Gaussian distributions such that
be the family of univariate Gaussian distributions such that 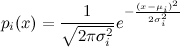
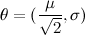 , the resultant Fisher Information matrix is computed to be
, the resultant Fisher Information matrix is computed to be 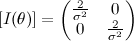 .
. can be reparametrized in terms of a single parameter
can be reparametrized in terms of a single parameter 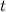 such that
such that 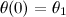 and
and 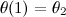 (I haven't computed this new parameter yet, but it shouldn't be difficult).
(I haven't computed this new parameter yet, but it shouldn't be difficult).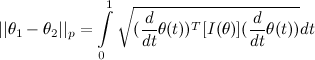 , which is given in closed form as
, which is given in closed form as 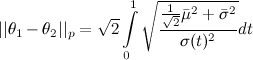 where
where 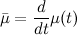 and
and 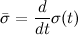 .
. 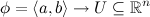
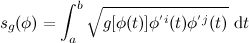

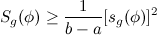
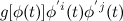 is constant in t.
is constant in t. 



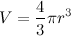 and the surface area of a sphere,
and the surface area of a sphere, 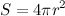 and a careful analysis of the properties of parabolas and other conics.
and a careful analysis of the properties of parabolas and other conics. for
for  .
.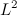 , which is quadratically integrable. Applying the special case of Jensen’s inequality using Measure-theoretic approach, you can show that
, which is quadratically integrable. Applying the special case of Jensen’s inequality using Measure-theoretic approach, you can show that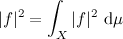
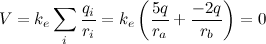
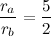



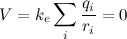
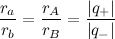 .
.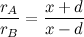
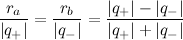 .
.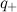 .
. 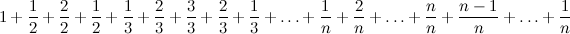
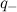 . The electric potential is zero ONLY when at the center of an electric dipole (a pair of electric charges of equal magnitude but of opposite sign or polarity).
. The electric potential is zero ONLY when at the center of an electric dipole (a pair of electric charges of equal magnitude but of opposite sign or polarity).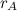 .
.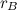 .
.
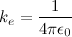 for simplification.
for simplification. 
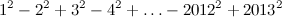 .
.
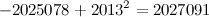
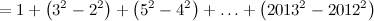
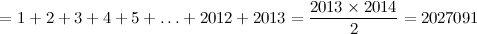
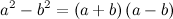 :
: 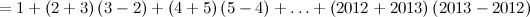
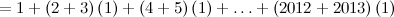
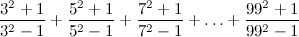 .
.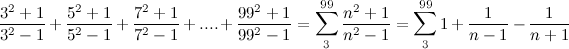
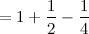
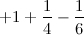
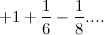
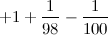
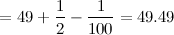
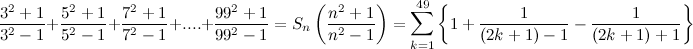
 , obtain the smallest value of
, obtain the smallest value of 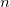 if the difference between the sum of the first
if the difference between the sum of the first 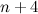 terms and the sum of the first
terms and the sum of the first 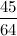 .
.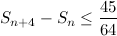
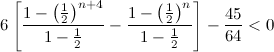 .
.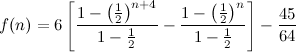 ,
,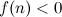



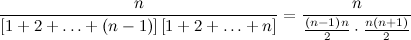








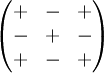
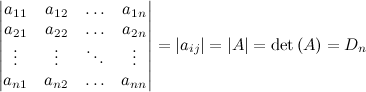
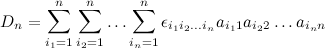
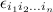 is the
is the 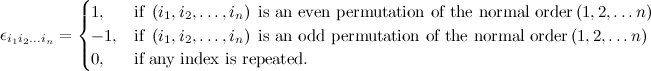


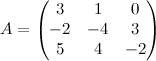 . Find det(A) by cofactor expansion.
. Find det(A) by cofactor expansion.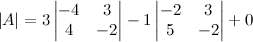
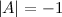

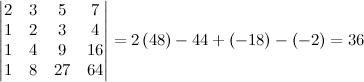

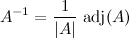
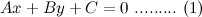
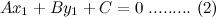
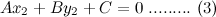
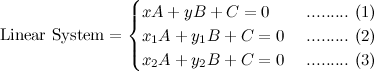
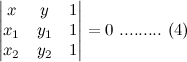
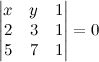
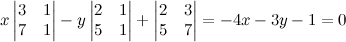
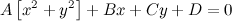
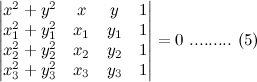
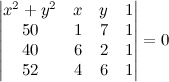
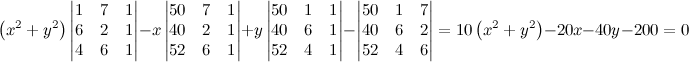

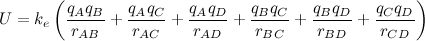

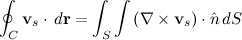



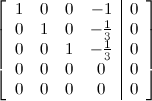



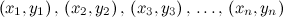
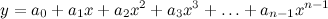
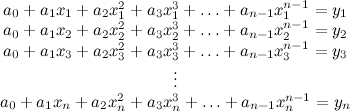
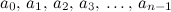 . From this point of view the augmented matrix for the system is
. From this point of view the augmented matrix for the system is
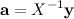 .
.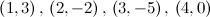
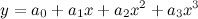
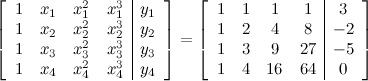

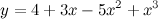



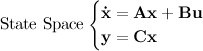
 to a desired final state
to a desired final state 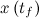 ; otherwise the system is said to be uncontrollable. In other words, an nth-order plant is completely controllable if the matrix
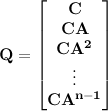
; otherwise the system is said to be uncontrollable. In other words, an nth-order plant is completely controllable if the matrix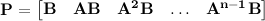



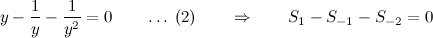
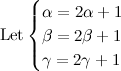
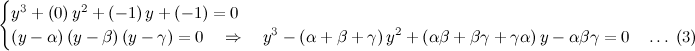
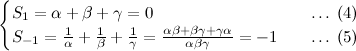
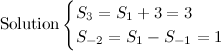
 0.2901sec
0.2901sec
 0.52
0.52
 6 queries
6 queries
 GZIP Disabled
GZIP Disabled