9th Dec 2013: Updated questions and answers...
OMK 2013 Sulong
Section A
1. A large cube is divided into 99 cubes with integer lengths, 98 of them with side 1. Find the volume of the large cube.
2. Let M be the set of all nine-digit positive integers that contain each digit from 1 to 9 once. Find the highest common factor of all elements of M.
3. What is the remainder when 5^5555 is divided by 10000?
4. Given a trapezium with perpendicular diagonals and height 12. The length of one of its diagonals is 15. Find the area of the trapezium.
5. The digits of 2013 can be rearranged to form an arithmetic progression. Determine the number of four-digit positive integers with this property.
(Note: An arithmetic progression might have common difference 0.)
6. Determine the smallest prime factor of 8051.
Section B
1. Given a triangle ABC. The midpoints of AB, BC, CA are C1, A1, B1 respectively.
Construct another triangle DEF with side lengths equal to the lengths of AA1, BB1, CC1.
(a) Prove that the ratio of the area of triangle DEF to the area of triangle ABC is a constant, regardless of the choice of triangle ABC.
(b) Find the area of triangle DEF if AB = 13, BC = 14, CA = 15.
2. Prove that there exist integers a1, a2, a3, …, a2013, b, all greater than 1, such that
(a1!)(a2!)(a3!)…(a2013!) = b!
3. A sequence x1, x2, x3, … is defined as follows: x1 = 1, x2 = 143, and
xn+1 = 5(x1 + x2 + … + xn)/n for all n ≥ 2.
Prove that all terms of the sequence are integers.
Hints & Answers:
» Click to show Spoiler - click again to hide... «
This post has been edited by ystiang: Dec 9 2013, 05:53 PM


 Aug 6 2013, 09:23 PM
Aug 6 2013, 09:23 PM
 Quote
Quote
 [/URL][/IMG]
[/URL][/IMG]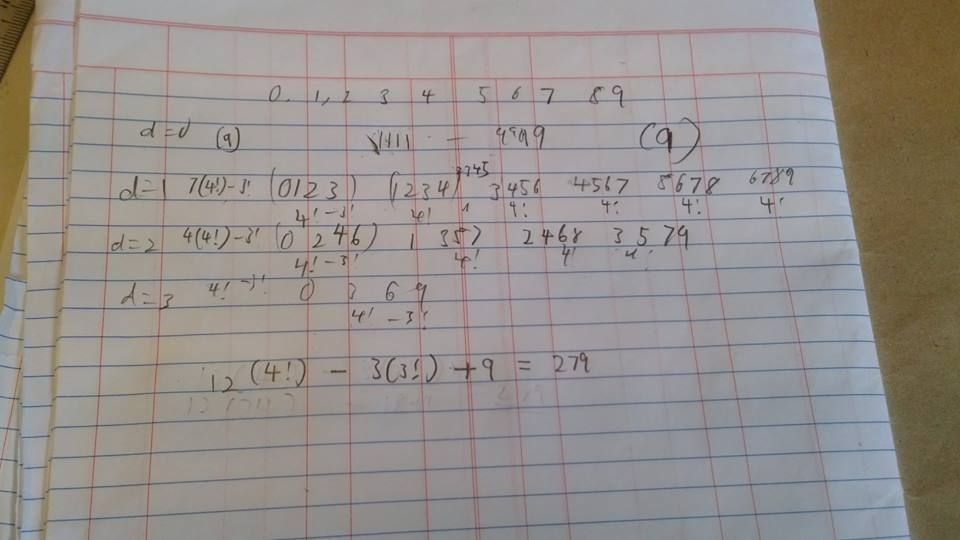 [/URL][/IMG]
[/URL][/IMG]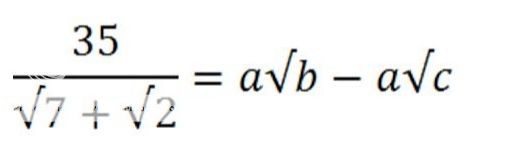
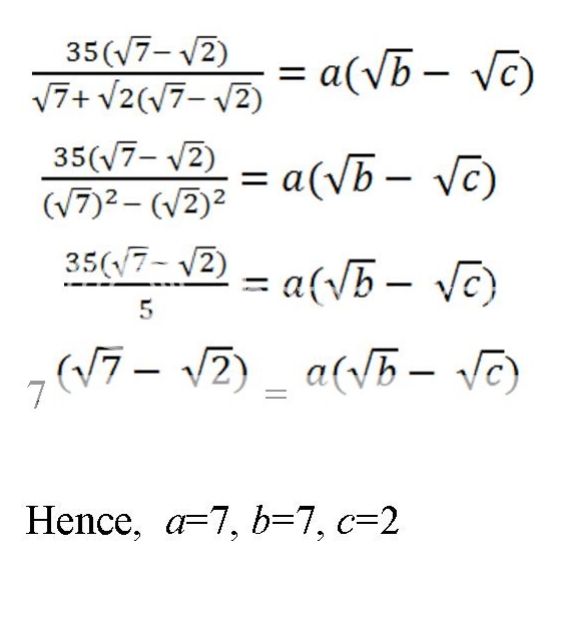
 , obtain the smallest value of
, obtain the smallest value of  if the difference between the sum of the first
if the difference between the sum of the first 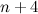 terms and the sum of the first
terms and the sum of the first 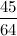 .
.
 0.0620sec
0.0620sec
 0.23
0.23
 7 queries
7 queries
 GZIP Disabled
GZIP Disabled