According to the First Law of Thermodynamics, your deduction in (1) is technically NOT wrong.
Consider one gram of water (1 cm³) becomes 1671 cm³ of steam when boiled at a constant pressure of 1 atm (101325 Pa). And the Latent heat of vaporization at this pressure is
.
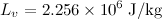
The work done by the water when it vaporizes is
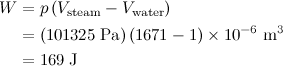
The heat added to the water is
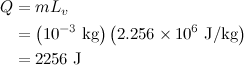
Internal energy is one of the most important concepts in thermodynamics, which we use the symbol U for internal energy. We
tentatively define the
internal energy of a system as the sum of the kinetic energies of all of its constituent particles, plus the sum of all the potential energies of interaction among these particles. In this example, the change in internal energy during phase change is
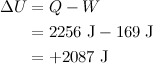
Here is the explanation: To vaporize 1 g of water, we must add 2256 J of heat, most of which (2087 J) remains in the system as an increase in internal energy (denoted by the positive sign). The remaining 169 J leaves the system as the system expands from liquid to vapor and does work against the surroundings. Boiling is an endothermic process because it absorbs energy to convert heat energy into chemical potential energy.
The increase in internal energy in boiling is associated mostly with the attractive intermolecular forces that hold the molecules together in the liquid state. It is represented by the breaking of bonds between molecules in the liquid state. This bond breaking allows the molecules to move farther apart in the gaseous state, with a corresponding
increase in intermolecular potential energy. The associated potential energies are greater after work has been done to pull the molecules apart, forming the vapor state. It’s like increasing gravitational potential energy by pulling an elevator farther from the center of the earth, U = mgh.
The fact that intermolecular forces decrease as you keep adding energy does not mean that potential energy decreases. The issue is that the change in potential energy is equal to the work you would have to do to vaporize the water against the intermolecular forces.
Now suppose you keep vaporizing until all the liquid water has been converted to steam. You still must apply constant heat into the system, so you are still doing work against the intermolecular forces. Therefore, the potential energy keeps increasing. As intermolecular forces get weaker and weaker, all that is happening is that
the rate at which potential energy is increasing is getting smaller. In other words, the more steam you vaporize, the greater the energy you must add to the system to achieve the same change in potential energy.
For the potential energy to start getting smaller as the water transforms to steam, intermolecular forces would have to reverse direction, but that never happens. What does happen is that as intermolecular distance approaches infinity, intermolecular forces approach zero, and the potential energy approaches a limiting value, but that value is far from zero if the reference level where PE = 0 is measured from Ice (solid) form (see diagram below). It is equal to all the work you did to melt the ice from solid to liquid water, and to vaporize water from liquid to gas (steam).
Because this limit exists, and because you are free to choose the state (either Ice or Steam) at which you call the potential energy zero, the zero level is sometimes chosen where the intermolecular distance approaches infinity. If you make that choice (like in
the case of an Ideal Gas), the potential energy of Ice is a hugely negative number. No matter how you define the zero level, the potential energy always increases during phase transformation from solid Ice to liquid Water, and from liquid Water to vapor Steam.
Aug 11 2013, 02:06 PM
[/URL][/IMG]
[/URL][/IMG]
Quote
Good idea to fill those 3 months .
But then what's the point of that?
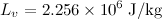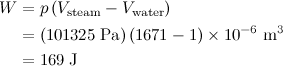
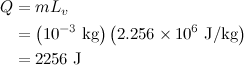
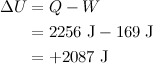
0.0489sec
0.42
7 queries
GZIP Disabled