Let's apply Polya’s four-step problem-solving process in this case.
STEP 1: Understand the problemSuppose that the cubic equation f(x) = ax³ + bx² + cx+ d = 0 has roots α, β, γ.
f(x) = ax³ + bx² + cx+ d = 0
x = α, β, γ
Find a new cubic equation g(x) with the roots h(α); h(β); h(γ).
Given: x = h(α); h(β); h(γ)
Find: g(x) = 0
STEP 2: Develop a plan to solve the problemRemainder and Factor Theorems tell us that: f(α) = f(β) = f(γ) = 0
Since g(x) = 0, we can apply the law of conservation of energy and we pick: g(x) = f(γ) = 0
Both sides must contain x. And the link between x and γ is x = h(γ). Manipulate it: γ = h^-1(x)
STEP 3: Carry out plang(x) = f(γ) = 0
g(x) = f[h^-1(x)] = 0
g(x) = px³ + qx² + rx+ s = 0
STEP 4: Look back and check the answer.The roots of the cubic equation px³ + qx² + rx+ s = 0 should be exactly the same as h(α); h(β); h(γ).
By the way, this sorcery is called “
by means of a substitution”, and the substitution is γ = h^-1(x) = 2x / (x − 1). Although this problem is inherently A-level / STPM level, it can be solved using SPM Form 4 Add Math Functions knowledge + Standard Algebraic Manipulations (SAM). Thanks
ystiang for he has done a good job!





 Nov 29 2013, 10:47 AM
Nov 29 2013, 10:47 AM

 Quote
Quote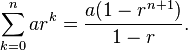



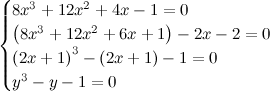
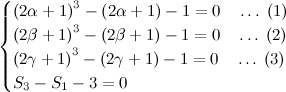

 0.0528sec
0.0528sec
 0.66
0.66
 7 queries
7 queries
 GZIP Disabled
GZIP Disabled