QUOTE(maximR @ Dec 15 2013, 09:35 PM)
I'm more geared towards Physics at the moment. This might change, that's why I'm keeping my options open.
Here is the Applied Physics based ACME network:

 Aerospace Engineering
Aerospace Engineering :: Aerodynamics, Aeroelasticity, Aerothermodynamics, Aerospace Structures, Flight Mechanics, Aircraft Stability & Control, Aircraft Design, Aircraft Fuel Systems, Air-breathing Propulsion, Avionics, Orbital Mechanics, Finite Element Analysis using Abaqus, Computational Fluid Dynamics using ANSYS, 3D CAD Design using CATIA
Civil Engineering :: Engineering Mechanics (Statics), Solid Mechanics, Materials Science, Structural Analysis & Design, Soil Mechanics, Fluid Mechanics, Hydraulics, Reinforced Concrete Design, Geotechnical Engineering, Environmental Engineering, Transportation Engineering, Water Resources Engineering, Construction Machinery, Computer-Aided Engineering Design using AutoCAD
Mechanical Engineering :: Engineering Mechanics (Statics & Dynamics), Mechanics of Materials, Materials Science, Thermodynamics, Tribology, Design of Machine Elements, Manufacturing Technology, Piston Machines, Pressure Vessels, Heat Exchangers, Turbomachinery, Computer-Aided Engineering Design using AutoCAD & Solidworks
Electrical Engineering :: RLC Circuits, AC Circuits, Filter Circuits, Three-Phase Circuits, Logic Circuits, Diodes, Transistors, Operational Amplifiers, Magnetic Circuits & Transformers, Applied Electromagnetics, DC Motors, AC Motors, Signal Processing, Communication Systems, Power Systems, Microelectronics, Intelligent Control Systems, Modeling, Simulation, Analysis, Design & Optimization of Systems using MATLAB & Simulink


 Dec 13 2013, 04:21 PM
Dec 13 2013, 04:21 PM Quote
Quote
 .
. is rational or irrational. Thus, we have two cases here.
is rational or irrational. Thus, we have two cases here. and raise it to the power of
and raise it to the power of  , so that
, so that  , that is obviously rational, which in turn proves the theorem is correct.
, that is obviously rational, which in turn proves the theorem is correct. .
. .
. , because when
, because when  ,
,  ,
,  , it follows that
, it follows that  .
. , Sum Rule
, Sum Rule 
 , Product Rule
, Product Rule 


 and
and 




 and
and  , Logarithmic Differentiation
, Logarithmic Differentiation




 by using the elementary row operation (ERO)?
by using the elementary row operation (ERO)?  , only a maximum of seven (ERO) operations are required to get
, only a maximum of seven (ERO) operations are required to get  . In fact, ERO is nothing simpler than the basic arithmetic operations + − × ÷. By the way, ERO is NOT a formula,
. In fact, ERO is nothing simpler than the basic arithmetic operations + − × ÷. By the way, ERO is NOT a formula, 
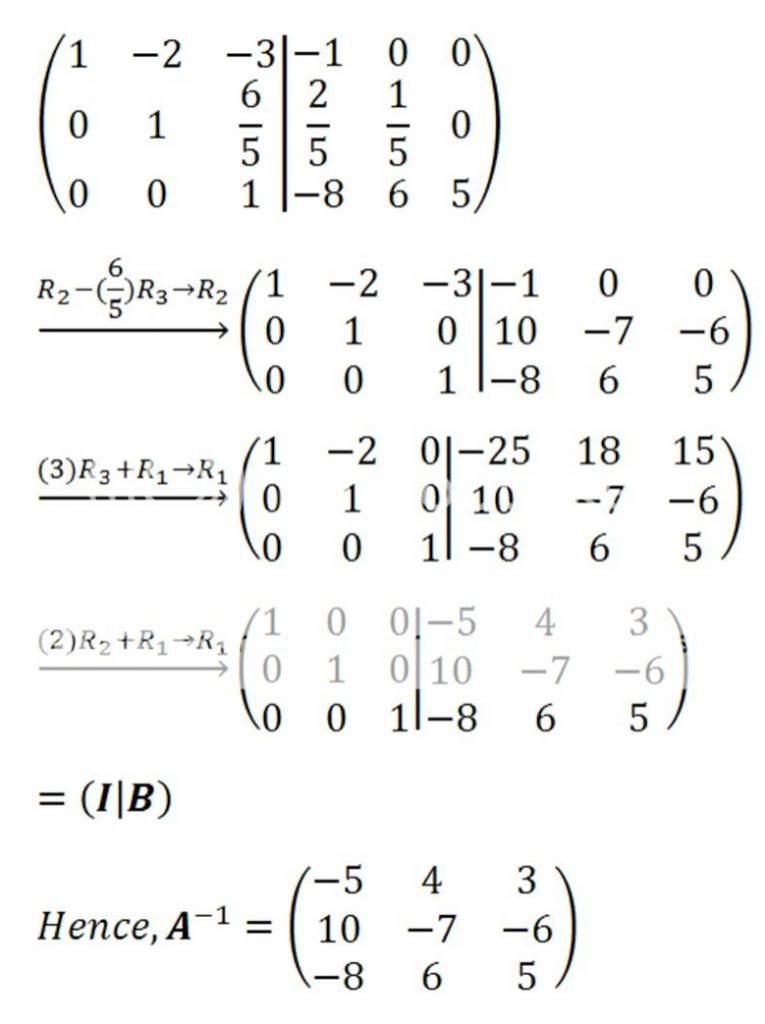



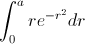
 .
. has no antiderivative, when you separate them by parts. The good news is that there is an easy way, called "
has no antiderivative, when you separate them by parts. The good news is that there is an easy way, called "

 0.0581sec
0.0581sec
 1.12
1.12
 7 queries
7 queries
 GZIP Disabled
GZIP Disabled