QUOTE(delsoo @ Dec 24 2013, 01:07 AM)
sorry i used to used to use 1/4pi e .... btw the rest are correct?
It's your preference. To answer the rest, please concentrate on reading my post CLOSELY. As mentioned in previous post. There is a mistake in (1), which is affecting (3) and (4).
(1) Find the electric potential at the point β (far right) due to a positively charged particle
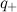 , separated by a distance
, separated by a distance 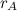 .
.You can substitute the positively charged particle
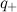 = 5q and the negatively charged particle
= 5q and the negatively charged particle 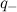 = -3q, as in your original problem in Post #396.
= -3q, as in your original problem in Post #396.This post has been edited by Critical_Fallacy: Dec 24 2013, 01:18 AM


 Dec 24 2013, 01:10 AM
Dec 24 2013, 01:10 AM Quote
Quote
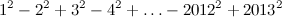 .
.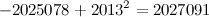
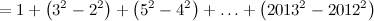
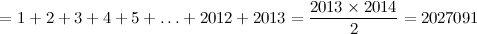
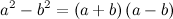 :
: 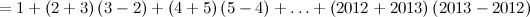
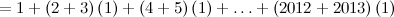
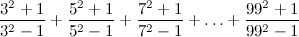 .
.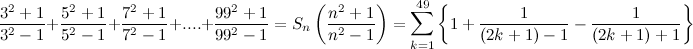
 , obtain the smallest value of
, obtain the smallest value of 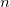 if the difference between the sum of the first
if the difference between the sum of the first 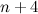 terms and the sum of the first
terms and the sum of the first 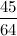 .
.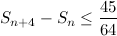
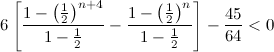 .
.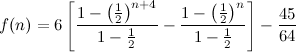 ,
,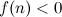


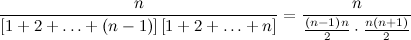






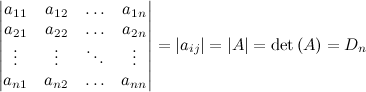
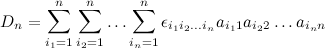
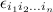 is the
is the 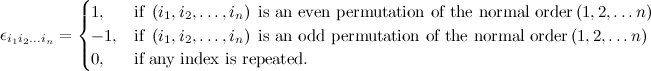


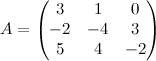 . Find det(A) by cofactor expansion.
. Find det(A) by cofactor expansion.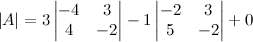
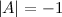

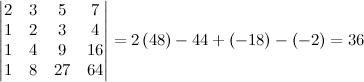
 0.0816sec
0.0816sec
 0.27
0.27
 7 queries
7 queries
 GZIP Disabled
GZIP Disabled