QUOTE(v1n0d @ Dec 22 2013, 10:51 AM)
P.S. Sorry for double posting, apparently there's a limit on how many images one can link in a single post.
You can post up to seven images in a single post.

QUOTE(v1n0d @ Dec 22 2013, 10:51 AM)
The distance for two distributions using the derived metric is given by
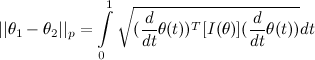
, which is given in closed form as
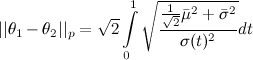
where
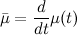
and
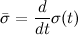
.
We define the
length with respect to the Riemann metric g of a piecewise continuously differentiable curve represented by a map
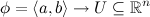
by the formula using Einstein convention
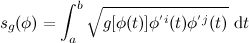
We see immediately that the Euler-Lagrange equation for the Riemann metric will be a pain because of the square root in the Lagrangian. But then, this problem has a surprisingly simple solution, which, at first, cannot possibly seem right: that is,
simply omit the square root! 
Thus, you probably want to consider the functional:

To justify this, recall a condition is called
parametrization by arc length, that if the functional Sg indeed has a minimum in the space of continuously differentiable curves with fixed boundary points A, B, then the minimum curve also minimizes the functional sg, and furthermore is parametrized by arc length! Therefore,
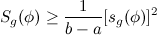
The
equality arises if and only if 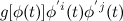
is constant in t.





 Dec 19 2013, 04:18 PM
Dec 19 2013, 04:18 PM Quote
Quote
 of a curve is to exploit the slope formula of a straight line.
of a curve is to exploit the slope formula of a straight line. , and the upper bound
, and the upper bound  .
. and
and  , a straight line
, a straight line  can be drawn, where it intercepts x-axis. The x value that intercepts x-axis is closer to the real root,
can be drawn, where it intercepts x-axis. The x value that intercepts x-axis is closer to the real root, 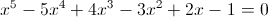 , and I guess it can't be solved, or perhaps I wasn't able to write down the root.
, and I guess it can't be solved, or perhaps I wasn't able to write down the root.



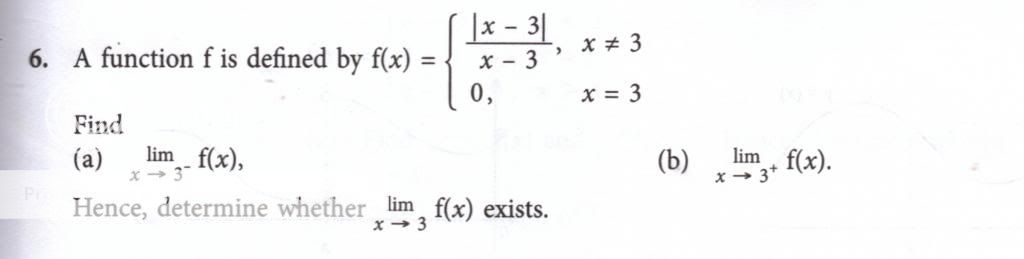



 approaches a different number from the right side of 3 than it approaches from the left side, the limit
approaches a different number from the right side of 3 than it approaches from the left side, the limit 
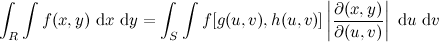
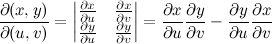
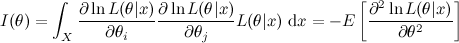
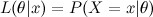
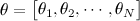 , the Fisher information takes the form of an N×N matrix as shown below.
, the Fisher information takes the form of an N×N matrix as shown below. 
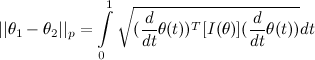 , which is given in closed form as
, which is given in closed form as 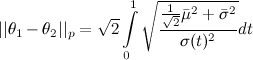 where
where 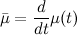 and
and 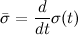 .
.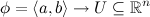
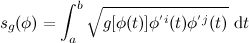

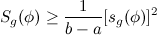
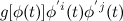 is constant in t.
is constant in t. 



 and the surface area of a sphere,
and the surface area of a sphere, 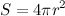 and a careful analysis of the properties of parabolas and other conics.
and a careful analysis of the properties of parabolas and other conics.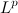 for
for 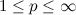 .
.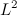 , which is quadratically integrable. Applying the special case of Jensen’s inequality using Measure-theoretic approach, you can show that
, which is quadratically integrable. Applying the special case of Jensen’s inequality using Measure-theoretic approach, you can show that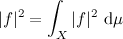
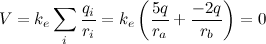
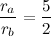



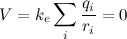
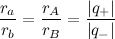 .
.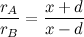
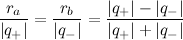 .
.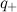 .
. 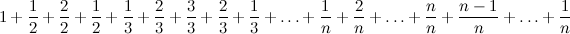
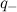 . The electric potential is zero ONLY when at the center of an electric dipole (a pair of electric charges of equal magnitude but of opposite sign or polarity).
. The electric potential is zero ONLY when at the center of an electric dipole (a pair of electric charges of equal magnitude but of opposite sign or polarity).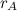 .
.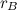 .
.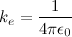 for simplification.
for simplification.  0.0653sec
0.0653sec
 0.99
0.99
 7 queries
7 queries
 GZIP Disabled
GZIP Disabled