QUOTE(scgoh123 @ Apr 13 2015, 07:00 PM)
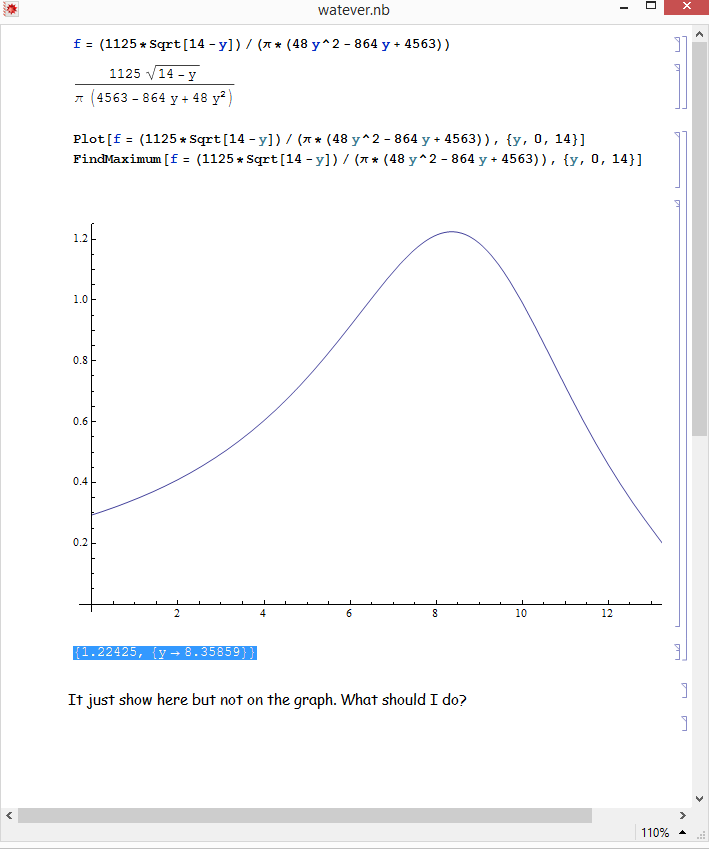
The problem that i had faced is when I tried to substitute h=14 into the differential equation that I have obtained, the time taken is infinity. The container will never be filled. So how do I calculate the time taken to fill up the container?
Was that really a problem? I believe that I've given an explanation in the previous post.
You could check your answer for h = 13.9 m and h = 13.99 m, to test the convergence of the result .
To make the problem more interesting, the parameters in part 2(b) should be chosen carefully k = 28 and n = 0.5, as both take roughly the same time (15.2 hours) to fill up the container up to the water level 13.9 m. But the nonlinear control mechanism in 2(b) will fill up the container 100% by 17 hours.
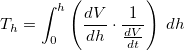
In reality, the process will be terminated (turn off the valve) if time taken to fill the container exceeds the expected time. The MRO (maintenance, repair, and overhaul) team will carry out the Fault Detection and Diagnosis manually on the system. Modern systems usually have the Fault-Tolerant Control System installed to minimize downtime of a system.
This post has been edited by Critical_Fallacy: Apr 13 2015, 09:39 PM


 Apr 13 2015, 09:16 PM
Apr 13 2015, 09:16 PM Quote
Quote

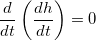 , it all goes back to the quadratics.
, it all goes back to the quadratics. 

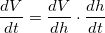 , find
, find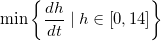
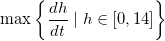
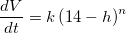 is given and
is given and 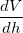 can be obtained from the derivative of 1(b), the rest is Algebra and you can find the
can be obtained from the derivative of 1(b), the rest is Algebra and you can find the 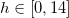 .
. 
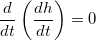
 0.0244sec
0.0244sec
 0.52
0.52
 6 queries
6 queries
 GZIP Disabled
GZIP Disabled