This is why I insisted you and
RED-HAIR-SHANKS to learn differential equations seriously and EARLY. You'll probably ask, Why differential equations? Why are they so important to deserve your attention?

Well, differential equations arise naturally as models in areas of science, engineering, economics, and lots of other subjects. Physical systems, biological systems, and economic systems; all these are marked by change, or dynamics. Differential equations model real-world systems by describing how they change. The unknown function y(t) could be the current in an electrical circuit, the concentration of a chemical undergoing reaction, the population of an animal species in an ecosystem, or the demand for a commodity in a micro-economy. Differential equations represent laws that dictate change, and the unknown y(t), for which we solve, describes exactly how the changes occur.
You don't have touch on Partial Differential Equation (PDE) at the moment until you learn Partial Differentiation later. Just focus on First-order ODEs and familiarize with solutions of ODEs. You'll need to learn to identify certain types of 1st-order ODEs such as Separable, Linear, Homogeneous, Bernoulli, and Riccati ODEs because different types have different techniques to solve them. After mastering Separation of Variables, the next one to learn is the integrating factor:
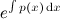
.
It may look complicated at first glance, but don't judge the formula by its Integral operator ∫.

Good question!

I purposely left out some explanations earlier, and you're up to my expectation. Here is the explanation:
This is just a prediction (but a good one), because an
educated guess (37°C) was made of the body’s temperature before death. It is also
impossible to keep the room at exactly 20°C (according to Fluid dynamics and Chaos theory). However, the model is
robust in the sense that small changes in the body’s normal temperature and in the constant temperature of the room yield
small changes in the estimated time of death. This can be verified by trying a slightly different normal temperature for the body, say 37.4°C, to see how much this changes the estimated time of death.
P.S.: A model is said to be
ROBUST if it can make “good” prediction under the worst-case conditions on the “
unknown unknowns” in the system dynamics. Robustness is of crucial importance in system modeling, because real dynamic and engineering systems are vulnerable to external disturbance and measurement noise, and there are always discrepancies between mathematical models used for calculation and the actual system in the real world.


 Jan 4 2014, 02:19 PM
Jan 4 2014, 02:19 PM

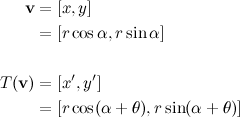

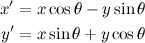
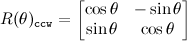



 Quote
Quote



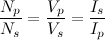
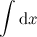 has no meaning. In the context of a separable differential equation however, it looks like this:
has no meaning. In the context of a separable differential equation however, it looks like this: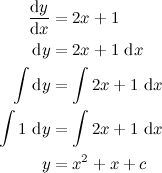
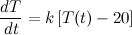 .
.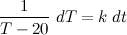
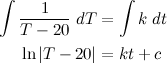
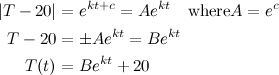
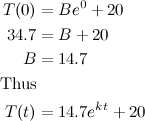
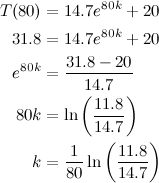
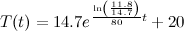

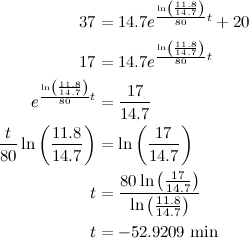
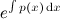 .
.






 0.0528sec
0.0528sec
 1.14
1.14
 7 queries
7 queries
 GZIP Disabled
GZIP Disabled