QUOTE(RED-HAIR-SHANKS @ Dec 18 2013, 10:22 PM)
I'm quite lucky to have bought that book. If you're looking for intense exercises that surpasses basic Form 6 Math, then Oxford Fajar would be it. I remembered that
Just Visiting By has previously mentioned somewhere that some of the exercises in Oxford Fajar are exceedingly tougher than Pelangi or Longman version of Math T books. Some of the questions are even beyond STPM level.....
Ya, some of the questions are too tough. You can do all the exercise in three books and make the comparison yourself.
QUOTE(RED-HAIR-SHANKS @ Dec 18 2013, 10:30 PM)
Not quite for Chemistry, except for Physics where I watched nearly all of the lecture videos of physics from an emeritus professor from MIT(Prof. Walter Lewin), his lectures were fantastic and lively

. But for now, the most intriguing part for me is Gravitation and Torque, albeit the fact that my insight concerning it is rather superficial. On some occasions, the videos from Khan Academy helps too

Gravitation is interesting. Torque is fine. Be worried about kinematics and dynamics. Although you've learnt all the concepts in SPM, STPM questions are much tougher. You can use your SPM level knowledge to do the first three chapters, all you need now is think better. Twist your brain harder.
Thermodynamics (kinetic theory of gases) is the most interesting for first term, at least to me.
QUOTE(RED-HAIR-SHANKS @ Dec 19 2013, 11:32 PM)
Thank you for posting your questions and also your guides on how to find the root of the quintic function. Well, actually I had a hard time cracking my brain in order to solve it. And most of all, I've failed to apply my knowledge of SPM level of Coordinate Geometry to find the root in this question. I've tried to delve a bit into this question, but, by using a different approach in order to find the x-value that is approaching to the real root.
At earlier of your posts, you gave me a tips by saying that the root occurs at f(x)=0. But, if we substitute 0 into y, we will get
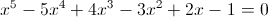
, and I guess it can't be solved, or perhaps I wasn't able to write down the root. I guess this has something to do with the Galois Theory, due to the fact that it's a quintic function. However, I can approximate the root by using Newton-Raphson method at least of it. Here it is:
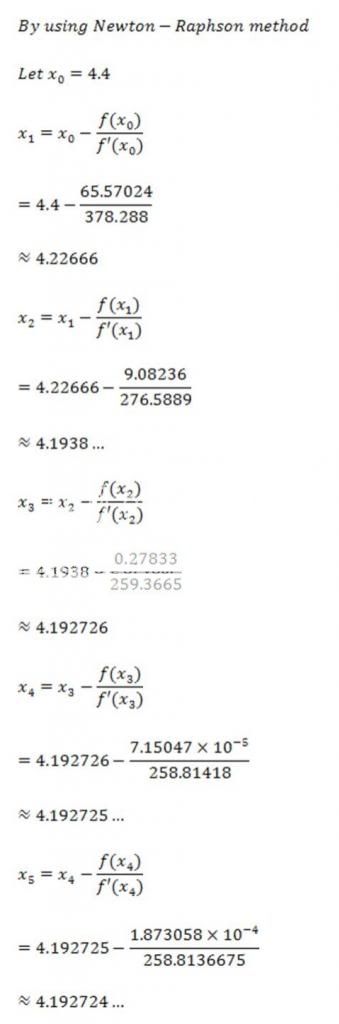
From my above workings, notice that three of the final values above is slightly similar, which is 4.19272. Hence, from here, we know that it's getting even more closer and closer to the real root. Correct me if I'm wrong.

Why delve so far into newton-raphson? In most cases, you can approximate the root by using trial and error. If the root involves decimal places, you can use either iteration method, newton-raphson or trapezium rule. However, for first term Maths, none of the calculus method is required. The roots are normally fractional or integral.
 Now that you've mentioned it, it seems true. It's due to the fact that when we are carrying out ERO, it will affect each row respectively, not by column. Ergo, if a supposed linear equation with unknown x, y and z is multiplied by a number H, the resulting equation will be Hx,Hy and Hz, which kinda resembles one of the 3 methods of ERO(Multiplying all the entries of a row by a scalar).
Now that you've mentioned it, it seems true. It's due to the fact that when we are carrying out ERO, it will affect each row respectively, not by column. Ergo, if a supposed linear equation with unknown x, y and z is multiplied by a number H, the resulting equation will be Hx,Hy and Hz, which kinda resembles one of the 3 methods of ERO(Multiplying all the entries of a row by a scalar).

 Dec 19 2013, 01:48 PM
Dec 19 2013, 01:48 PM

 Quote
Quote


 of a curve is to exploit the slope formula of a straight line.
of a curve is to exploit the slope formula of a straight line. , and the upper bound
, and the upper bound  .
. and
and  , a straight line
, a straight line  can be drawn, where it intercepts x-axis. The x value that intercepts x-axis is closer to the real root,
can be drawn, where it intercepts x-axis. The x value that intercepts x-axis is closer to the real root, 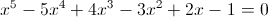 , and I guess it can't be solved, or perhaps I wasn't able to write down the root. I guess this has something to do with the Galois Theory, due to the fact that it's a quintic function. However, I can approximate the root by using Newton-Raphson method at least of it. Here it is:
, and I guess it can't be solved, or perhaps I wasn't able to write down the root. I guess this has something to do with the Galois Theory, due to the fact that it's a quintic function. However, I can approximate the root by using Newton-Raphson method at least of it. Here it is: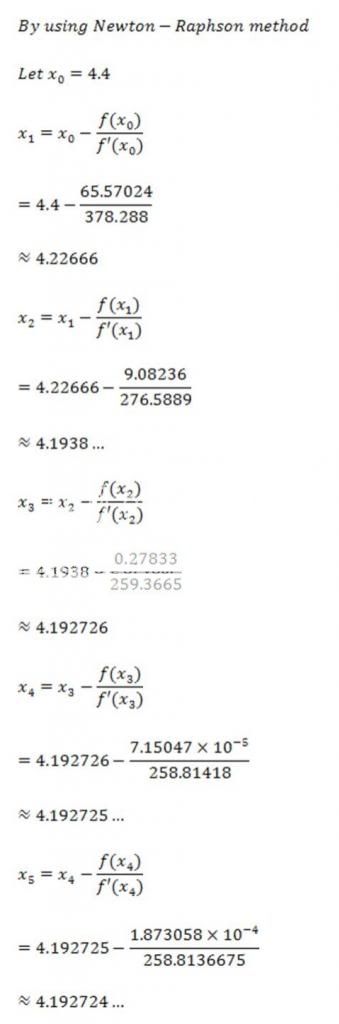




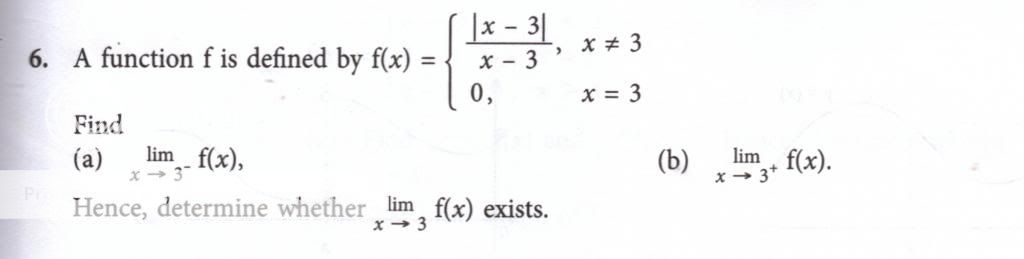



 approaches a different number from the right side of 3 than it approaches from the left side, the limit
approaches a different number from the right side of 3 than it approaches from the left side, the limit 
 0.0371sec
0.0371sec
 0.84
0.84
 6 queries
6 queries
 GZIP Disabled
GZIP Disabled