QUOTE(delsoo @ Jan 26 2014, 06:06 PM)
for this question why there's not 2 time constant during 0.04 till 0.06 s ?
Could you rephrase your question with clarity, please?2τ = 0.02 sec
Ask a Mathematical Physicist
|
|
 Jan 26 2014, 06:46 PM Jan 26 2014, 06:46 PM
Return to original view | Post
#261
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(delsoo @ Jan 26 2014, 06:06 PM) for this question why there's not 2 time constant during 0.04 till 0.06 s ? Could you rephrase your question with clarity, please?2τ = 0.02 sec |
|
|
|
|
|
 Jan 26 2014, 07:35 PM Jan 26 2014, 07:35 PM
Return to original view | Post
#262
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(Akatsuki0895 @ Jan 26 2014, 07:05 PM) 1)Determine whether this mapping is a function: DEFINITION ::x |--->the length of the line from the origin to (0,x),x element of real numbers the answer is no...but i don't really understand the question and the answer. Let X and Y be sets of real numbers. A real-valued function of a real variable, x from X to Y is a correspondence that assigns to each number x in X exactly one number y in Y. |
|
|
 Jan 26 2014, 08:44 PM Jan 26 2014, 08:44 PM
Return to original view | Post
#263
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
|
|
|
 Jan 26 2014, 08:54 PM Jan 26 2014, 08:54 PM
Return to original view | Post
#264
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(delsoo @ Jan 26 2014, 08:37 PM) i mean when time =0.04 to 0.06s, why power of e is not 2 since 0.04 to 0.06 is 2 time constant ... Typo error. Moreover, it doesn't show the full workings because the author assumes all readers have strong algebra basics. But the graph is correctly sketched. Perhaps you should show your workings here. |
|
|
 Jan 26 2014, 11:21 PM Jan 26 2014, 11:21 PM
Return to original view | Post
#265
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(delsoo @ Jan 26 2014, 11:04 PM) I mean -x to.the power of 2. Ps I.haven't learn integration. Perhaps you can correct me ∂soo,Your answer −x² is correct. My point is, you must have a basis to find the anti-derivative of −2x if you want to evaluate ∫ (−2x) dx. Please share with me, what Differentiation Rule did you use? Type out the formula in LaTeX for clarity. The more you figure out yourself, the better you learn math. I'm just guiding you. |
|
|
 Jan 27 2014, 10:09 PM Jan 27 2014, 10:09 PM
Return to original view | Post
#266
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(ystiang @ Jan 27 2014, 05:27 PM) can you teach me how to space out in mathURL LaTeX input? I tend to use these two for spacing:x \quad y →  x\; y → 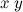 http://en.wikipedia.org/wiki/Help:Displayi...formula#Spacing |
|
|
|
|
|
 Jan 27 2014, 10:18 PM Jan 27 2014, 10:18 PM
Return to original view | Post
#267
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(maximR @ Jan 27 2014, 02:27 PM) Physics questions Not 216 N? Q1. Hailstones with an average mass of 0.04 kg fall vertically and strike a flat roof at 12 m/s. In a period of 5.0 minutes, 6 000 hailstones fall on each square metre of roof and rebound vertically at 3.0 m/s. Calculate the force on the roof if it has an area of 30 m^2. QUOTE(maximR @ Jan 27 2014, 02:27 PM) Q2. You don't need to find the angle of inclination θ because you can determine cos θ and sin θ from the Pythagorean theorem. The hypotenuse is 20 m and altitude (height) is 1 m. A car of mass 1 000 kg tows a caravan of mass 600 kg up a road which rises 1 m vertically for every 20 m of its length. There are constant frictional resistances of 200 N and 100 N to the motion of car and caravan respectively. The combination has an acceleration of 1.2 m/s^2 with the engine exerting a constant driving force. Assume that g = 10 m/s^2. Find : (a) the driving force , (b) the tension in the tow bar |
|
|
 Jan 27 2014, 11:12 PM Jan 27 2014, 11:12 PM
Return to original view | Post
#268
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(maximR @ Jan 27 2014, 02:27 PM) Mathematics questions ninty and ystiang have already covered this. Q1. The interval on which the function f(x) = log1/2 (x^2 - 2x - 3) is monotone increasing is ( ) ? QUOTE(maximR @ Jan 27 2014, 02:27 PM) Q2. Where did you get this question at A-level? If real numbers satisfy (x + 5)² + (y − 12)² = 14², then the minimum value of x² + y² is ( ) ? 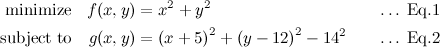 where (x, y) is a 2-dimensional vector called the design vector, f(x,y) is termed the objective function, and g(x,y) = 0 is known as the equality constraint. There are few methods to solve it such as the popular Lagrange multiplier method and the Direct Substitution method, but I prefer the Solution by the method of Constrained Variation. The basic idea is to find a closed-form expression for the first-order differential of f(df) at all points at which the constraint is satisfied. The desired optimum points are then obtained by setting the differential df equal to zero, that is introduced without proof: 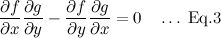 Equation (2) can be rewritten as 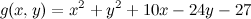 So we have 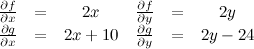 Equation (3) gives 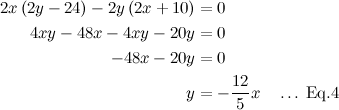 The optimum values of x can be obtained substituting Eq.(4) into Eq.(2): 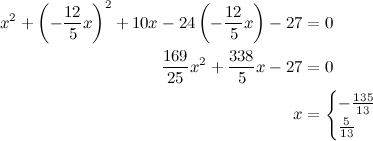 The optimum values of y can be obtained from Eq.(4): 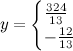 The optimum values of function f can be obtained from Eq.(1): 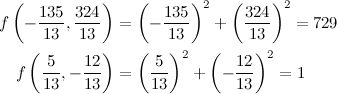 This solution gives the minimum value of x² + y² as 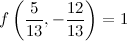 REMARK :: ------------- Please note that f(x,y) = x² + y² is an infinite paraboloid in a 3-D plot. The constraint g(x,y) is the dark blue circle in the contour plot. The objective is to find the minimum value of f(x,y) around the constrained geometry g(x,y). From the contour plot, you can also estimate the maximum value of f(x,y) occurs at somewhere near x = -10 and y = 25 (see the lighter band).  This post has been edited by Critical_Fallacy: Jan 28 2014, 09:00 AM |
|
|
 Jan 28 2014, 09:55 AM Jan 28 2014, 09:55 AM
Return to original view | Post
#269
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(maximR @ Jan 27 2014, 02:27 PM) Q2. Using SPM Calculus, you can solve it by Direct Substitution.If real numbers satisfy (x + 5)² + (y − 12)² = 14², then the minimum value of x² + y² is ( ) ? If we choose to eliminate y from Equation (1): f(x,y), then Equation (2): g(x,y) gives 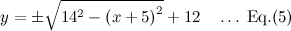 Thus the objective function f(x,y) becomes 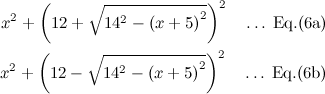 Plotting Equation (6a):  Plotting Equation (6b):  The desired optimum points are then obtained by setting the derivative df/dx of Eq.(6a) & Eq.(6b) equal to zero. 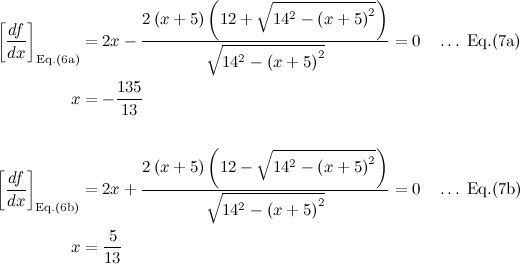 The optimum values of y can be obtained from Eq.(5): 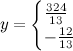 The optimum values of function f can be obtained from Eq.(1): 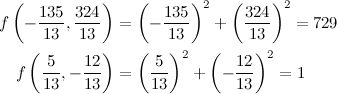 This solution gives the minimum value of x² + y² as 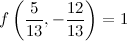 |
|
|
 Jan 28 2014, 10:43 PM Jan 28 2014, 10:43 PM
Return to original view | Post
#270
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(maximR @ Jan 28 2014, 08:57 PM)   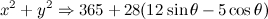 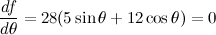 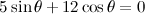 Solution 1: long version 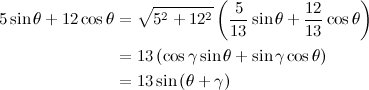 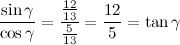 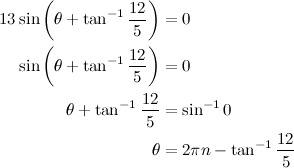 Solution 2: short version 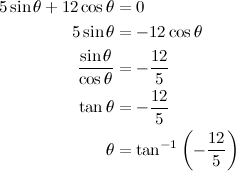 |
|
|
 Feb 3 2014, 05:27 PM Feb 3 2014, 05:27 PM
Return to original view | Post
#271
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(maximR @ Feb 2 2014, 10:32 PM) A car of mass 1 000 kg tows a caravan of mass 600 kg up a road which rises 1 m vertically for every 20 m of its length. There are constant frictional resistances of 200 N and 100 N to the motion of car and caravan respectively. The combination has an acceleration of 1.2 m/s^2 with the engine exerting a constant driving force. Assume that g = 10 m/s^2. Find : 恭喜发财,马到成功!(a) the driving force , (b) the tension in the tow bar Krevaki Help please? To solve this problem, you have to develop the equations of motion which require a relationship between the forces acting on a particle and the accelerated motion they cause.  The general technique is to write down the equation you get by applying Newton’s 2nd law to the combined particle ‘car + caravan’, and then solve the equation for the unknown. To do that, you are advised to draw separate force diagrams for car and caravan. Drawing this diagram is very important since it provides a graphical representation that accounts for all the forces which act on the particle, and thereby makes it possible to resolve these forces into their x, y components in 2-D.  It is also common to assume in a model like this that the tow bar is inextensible. That means it will not stretch. For mathematical convenience, we generally assume that the sense of each acceleration component acts in the same direction of as its positive inertial coordinate axis (denoted by the right-arrow notation → for horizontal axis, and the up-arrow notation ↑ for vertical axis).  I do one example (Part B). We are mainly concerned with the horizontal components because we want to determine the tension T. Ask Krevaki or kingkingyyk to check! 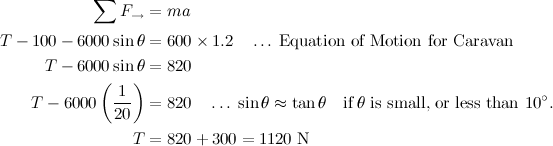 This post has been edited by Critical_Fallacy: Feb 3 2014, 09:19 PM |
|
|
 Feb 4 2014, 12:02 PM Feb 4 2014, 12:02 PM
Return to original view | Post
#272
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(maximR @ Feb 3 2014, 10:07 PM) Thank you Critical_Fallacy and kingkingyyk, and 恭喜发财 to you too! CLASSIC PROBLEMS ::The main objective is to help you to develop the ability to analyze classic problems in a simple and logical manner and to apply to its solution a few, well-understood, basic Physics principles. Question 1 The two blocks shown start from rest. The horizontal plane and the pulley are frictionless, and the pulley is assumed to be of negligible mass. Determine the acceleration of each block and the tension in each cord.  (Ans :: a_A = 8.40 m/s², a_B = 4.20 m/s², T_ADC = 840 N, T_CB = 1680 N) Question 2 The bob of a 2-m pendulum describes an arc of circle in a vertical plane. If the tension in the cord is 2.5 times the weight of the bob for the position shown, find the velocity and the acceleration of the bob in that position.  (Ans :: a_T = 4.90 m/s², a_N = 16.03 m/s², v = ±5.66 m/s) Question 3 Determine the rated speed of a highway curve of radius r = 125 m banked through an angle u = 18°. The rated speed of a banked highway curve is the speed at which a car should travel if no lateral friction force is to be exerted on its wheels.  (Ans :: 71.8 km/h) |
|
|
 Feb 5 2014, 08:31 AM Feb 5 2014, 08:31 AM
Return to original view | Post
#273
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(delsoo @ Feb 3 2014, 09:12 PM) Hi all I have. No idea on how to get the asymptotes for the graph of y square. By the definition of asymptotes, when both x and y become very large, the equation 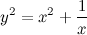 approximates to approximates to 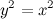 (also can be rearranged to (also can be rearranged to 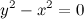 ), since ), since 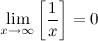 . .But using the difference of squares formula, 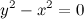 is also the equation of two straight lines is also the equation of two straight lines 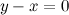 and and 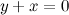 . .So, for large values of x and y, the graph approximates to a pair of straight lines. Hence, the pair of lines 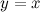 and and 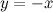 are the asymptotes of the graph. are the asymptotes of the graph.  |
|
|
|
|
|
 Feb 5 2014, 08:43 AM Feb 5 2014, 08:43 AM
Return to original view | Post
#274
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
Hi delsoo,
If you look closely at the equation 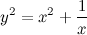 , y tends to become very large when x approaches to 0, because , y tends to become very large when x approaches to 0, because 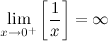 . Therefore, the third asymptote is a vertical line . Therefore, the third asymptote is a vertical line 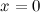 . .  |
|
|
 Feb 5 2014, 04:39 PM Feb 5 2014, 04:39 PM
Return to original view | Post
#275
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(Krevaki @ Feb 5 2014, 10:56 AM) My answer agrees with the ones obtained by kingkingyyk and Critical_Fallacy, but that is assuming I interpret the question in the same way. However, can I interpret "for every 20 m of its length" as the hypotenuse since the combination is being driven "up a road"? You are correct! The length of the hypotenuse is 20 m. I overlooked this when I sketched the diagram. p/s: It is still Lunar New Year, I would like to enjoy it while I still can. |
|
|
 Feb 6 2014, 12:27 AM Feb 6 2014, 12:27 AM
Return to original view | Post
#276
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(delsoo @ Feb 3 2014, 09:57 PM) If k=-1 then how can the function have 2 roots?? Since it only intersect the graph at 1 point Obviously the graph has only one real root (or repeated root) at x = 0. The question does not specify the number of real roots. The solution given is a graphical method. If you sketch the graph nicely and understand how a function works, this approach is easy.   Otherwise, go for the analytical method in Post #870. This post has been edited by Critical_Fallacy: Feb 6 2014, 10:17 AM |
|
|
 Feb 6 2014, 10:17 AM Feb 6 2014, 10:17 AM
Return to original view | Post
#277
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(delsoo @ Feb 5 2014, 11:50 PM) Critical_Fallacy thanks for your explaination! I can understand it now! can you expalin post#859 pls? This is analytical method: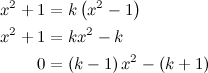 If a (coefficient of x²) is nonzero, the condition for having real roots: 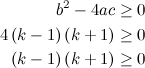 Find the k-values that satisfy the inequality. 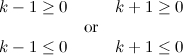 Results: 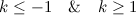 But what defines a (coefficient of x²) is k − 1. Since a must be nonzero, therefore 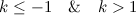 |
|
|
 Feb 6 2014, 04:51 PM Feb 6 2014, 04:51 PM
Return to original view | Post
#278
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
 Interesting question from VengenZ! Must invite kingkingyyk, Krevaki, ninty, v1n0d, ystiang. It can be shown that 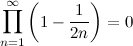 and 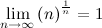 I think the question is to find 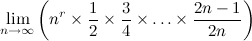 This post has been edited by Critical_Fallacy: Feb 6 2014, 04:56 PM |
|
|
 Feb 7 2014, 02:22 PM Feb 7 2014, 02:22 PM
Return to original view | Post
#279
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(acgerlok7 @ Feb 7 2014, 01:09 PM) if not, i feel like im actually requesting to be spoonfeed.. Spoon-feed is to feed (someone) by using a spoon. But I feed using thought-provoking words. |
|
|
 Feb 8 2014, 05:41 PM Feb 8 2014, 05:41 PM
Return to original view | Post
#280
|
|
VIP
3,713 posts Joined: Nov 2011 From: Torino |
QUOTE(maximR @ Feb 7 2014, 06:52 PM) Q1. Particle A moves with kinetic energy E and momentum p. It collides elastically with particle B which is at rest. After collision the particles move together. Calculate : Perhaps you can imagine the collisions between billiard balls. If they “collide elastically” the colliding particles do not stick together. What do you mean by “move together”?a) the kinetic energy of A and total kinetic energy of the system after collision b) the magnitude of momentum of A and of the system after collision  |
| Change to: |  0.0610sec 0.0610sec
 0.33 0.33
 7 queries 7 queries
 GZIP Disabled GZIP Disabled
Time is now: 24th December 2025 - 04:38 AM |