QUOTE(maximR @ Dec 15 2013, 10:21 PM)
Pure and Industrial. Pure has more focus on analytical subjects such as topology and set theory, industrial focuses on statistics and mathematical physics.Ask a Mathematical Physicist
Ask a Mathematical Physicist
|
|
 Dec 15 2013, 10:25 PM Dec 15 2013, 10:25 PM
Return to original view | Post
#21
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
|
|
|
|
|
|
 Dec 18 2013, 07:53 PM Dec 18 2013, 07:53 PM
Return to original view | Post
#22
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(RED-HAIR-SHANKS @ Dec 18 2013, 07:15 PM) Here, these are my workings, but I think they're incomplete: Your work is incomplete, you have generated what's called a row echelon matrix (REM). To obtain the inverse, you need to keep reducing the matrix on the left to reduced row echelon form (RREM). My problem arouse when I am unable to obtain zero in all three of the entries that is above the leading diagonal(above all the 1's). I'm in deadlock. Use the third row to eliminate the third column in rows 1 and 2. Then use the 2nd row to eliminate the second column in row 1. |
|
|
 Dec 19 2013, 05:27 PM Dec 19 2013, 05:27 PM
Return to original view | Post
#23
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(Critical_Fallacy @ Dec 19 2013, 03:30 PM) Whether Shanks simplifies Rows 1 & 2 or not, it doesn't really matter, because the ultimate objective is to normalize all diagonal elements. It does not change the fact that Shanks still can reduce the augmented matrix to row echelon form within the minimum 6 STEPS in Gauss Elimination of a 3-by-3 matrix. before performing the back-substitution. Simplification and normalizing the diagonal elements each have their own uses. For numerical work, the diagonal normalization reduces the number of operations required to obtain the inverse. In programming, this is the better approach because it cuts down on computing time. However, if the matrix is littered with unknown variables (such as algebraic expressions in lieu of numbers), it's not always the best idea to introduce fractions. In the case of exam questions, more often than not a matrix with unknown variables in it is reducible to a simpler form just by playing around with the rows. My advice is examine the matrix first and then decide which method is better. |
|
|
 Dec 20 2013, 05:16 PM Dec 20 2013, 05:16 PM
Return to original view | Post
#24
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(iChronicles @ Dec 20 2013, 02:28 PM) For parts (a) and (b), you will need to either:* sketch the graph of f(x) for some interval containing the value x=3 (say 0<x<6) OR * draw a table and compute values of f(x) as they approach from the negative and positive directions (compute f(x) for values of x=2.8,2.9,3.1,3.2 etc.) The third part is easily completed by recalling that the limit exists at a point if the limits from the positive and negative direction are equal to each other, i.e. f(x) has a limit at x=3 if your results for (a) and (b) are the same. P.S. Critical_Fallacy I tried using the TeX editor in your siggy, but it seems quite tedious. Do you upload each image to Imgur or am I doing it wrong? |
|
|
 Dec 21 2013, 11:50 AM Dec 21 2013, 11:50 AM
Return to original view | Post
#25
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
I was pleasantly surprised this morning when I got up to see the whole lot of you rallying behind getting TeX support for our forum. Thanks guys!
For the time being, we'll make do with the online service that wKkaY suggested. The link to it is in Critical_Fallacy's siggy. On a separate note, Critical_Fallacy are you familiar with integration over matrices? I need to compute the Riemannian metric over the Fisher matrix but I'm totally lost. |
|
|
 Dec 22 2013, 10:50 AM Dec 22 2013, 10:50 AM
Return to original view | Post
#26
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(Critical_Fallacy @ Dec 22 2013, 01:41 AM) To integrate a matrix of this size N, all we do is integrate the individual entries, which can be quite tedious. This is the portion that's killing me. Let me give an example of what's been done so far:Let 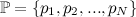 be the family of univariate Gaussian distributions such that be the family of univariate Gaussian distributions such that 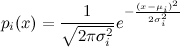 Taking the parametrization 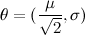 , the resultant Fisher Information matrix is computed to be , the resultant Fisher Information matrix is computed to be 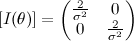 . .Now the distance between two distributions can be computed using the induced Reimannian metric provided  can be reparametrized in terms of a single parameter can be reparametrized in terms of a single parameter 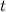 such that such that 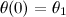 and and 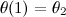 (I haven't computed this new parameter yet, but it shouldn't be difficult). (I haven't computed this new parameter yet, but it shouldn't be difficult). |
|
|
|
|
|
 Dec 22 2013, 10:51 AM Dec 22 2013, 10:51 AM
Return to original view | Post
#27
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
Now comes the part where I'm stuck:
The distance for two distributions using the derived metric is given by 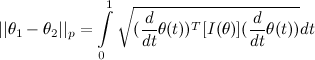 , which is given in closed form as , which is given in closed form as 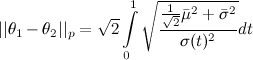 where where 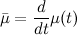 and and 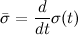 . . P.S. Sorry for double posting, apparently there's a limit on how many images one can link in a single post. |
|
|
 Dec 22 2013, 11:01 PM Dec 22 2013, 11:01 PM
Return to original view | Post
#28
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(Critical_Fallacy @ Dec 22 2013, 02:15 PM) You can post up to seven images in a single post. Do you have a link to any material on this? I mean the equivalence of minimizing a function as compared to its square root.We define the length with respect to the Riemann metric g of a piecewise continuously differentiable curve represented by a map 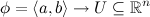 by the formula using Einstein convention 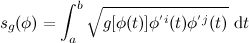 We see immediately that the Euler-Lagrange equation for the Riemann metric will be a pain because of the square root in the Lagrangian. But then, this problem has a surprisingly simple solution, which, at first, cannot possibly seem right: that is, simply omit the square root! |
|
|
 Dec 23 2013, 12:35 PM Dec 23 2013, 12:35 PM
Return to original view | Post
#29
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(Critical_Fallacy @ Dec 23 2013, 11:04 AM) It probably be pretty tedious for me to type the proof here. But it doesn't matter because the concept is about applying Jensen’s inequality to a Lebesgue-integrable function, Cool, thanks! 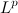 for for 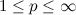 . .When p = 2, it becomes 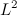 , which is quadratically integrable. Applying the special case of Jensen’s inequality using Measure-theoretic approach, you can show that , which is quadratically integrable. Applying the special case of Jensen’s inequality using Measure-theoretic approach, you can show that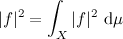 For more information, you can find various articles online on 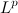 spaces, Jensen’s inequality, Hölder’s inequality, and Minkowski’s inequality. spaces, Jensen’s inequality, Hölder’s inequality, and Minkowski’s inequality. I work with measure as well, but I've not come across Jensen's inequality before. Will look into it. |
|
|
 Dec 25 2013, 10:50 AM Dec 25 2013, 10:50 AM
Return to original view | Post
#30
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
Alternating series are generally more fun to work with, because the terms sometimes cancel out, resulting in a very simple solution.
Since we're on the subject of series, do try this one: For the geometric series  , obtain the smallest value of , obtain the smallest value of 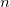 if the difference between the sum of the first if the difference between the sum of the first 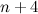 terms and the sum of the first terms and the sum of the first 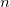 terms is less than terms is less than 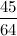 . .This is an STPM Mathematics T Paper 1 question from 2009. This post has been edited by v1n0d: Dec 25 2013, 10:51 AM |
|
|
 Dec 26 2013, 08:15 AM Dec 26 2013, 08:15 AM
Return to original view | Post
#31
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(Flame Haze @ Dec 25 2013, 01:13 PM) QUOTE(ystiang @ Dec 25 2013, 05:37 PM) A standard way to solve this type of problem in STPM, taking the logarithm at both sides: The answer is 5, yes.» Click to show Spoiler - click again to hide... « Hence, the least value of n is 5. ystiang provides the standard answer as according to the answer scheme, but it's worth noting that there is more than one method that can be applied, as shown by Critical_Fallacy. Depending on the seniority of the teacher marking your paper, the alternative method may/may not be accepted (younger teachers tend to be very rigid when it comes to marking papers according to the answer scheme given). The only time that an answer is to strictly follow a specific method is when you see the word "hence" in the question, which implies that you MUST use the results from the previous section (either an equality or a graph) to deduce your answer. |
|
|
 Dec 30 2013, 08:19 AM Dec 30 2013, 08:19 AM
Return to original view | Post
#32
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
Wow. AFK for a couple of days and so much has been discussed!
|
|
|
 Jan 1 2014, 10:16 AM Jan 1 2014, 10:16 AM
Return to original view | Post
#33
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(Critical_Fallacy @ Dec 31 2013, 05:28 PM) Haha! Looking at the choice of variables and your previous 2013 question, I figured it'd be a new year wish!Looks like ystiang has beat me to the answer though. |
|
|
|
|
|
 Jan 1 2014, 11:44 PM Jan 1 2014, 11:44 PM
Return to original view | Post
#34
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(maximR @ Jan 1 2014, 04:06 PM) Lolwut?QUOTE(maximR @ Jan 1 2014, 10:37 PM) This is what matters in life. The best job a person can have is one that's also your hobby. |
|
|
 Jan 3 2014, 01:09 AM Jan 3 2014, 01:09 AM
Return to original view | Post
#35
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(danny88888 @ Jan 2 2014, 10:31 PM) Assume that the equation system x*2 + sxy + y*2 - 1 = 0; x*2 + y*2 - s*2 + 3 = 0 defi ne x and y implicitly as differentiable functions of s. (a) Differentiate the system (i.e. fi nd the differentials) and fi nd the values of x'(s) =dx/ds and y'(s)= dy/ds when x=0, y=1 and s=2 Can someone give me an insight of this? QUOTE(Critical_Fallacy @ Jan 2 2014, 11:59 PM) Is sxy really just sxy? I feel like there's something missing.This post has been edited by v1n0d: Jan 3 2014, 01:10 AM |
|
|
 Jan 3 2014, 09:27 AM Jan 3 2014, 09:27 AM
Return to original view | Post
#36
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(danny88888 @ Jan 3 2014, 01:29 AM) Differentiating the first equation, we obtain: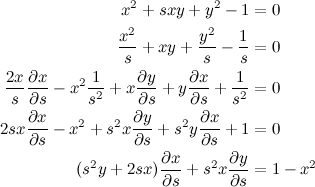 (1) (1)Differentiating the second equation, we obtain: 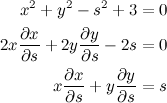 (2) (2)Now all that's left is to substitute equations 1 into 2 (or vice versa) to form 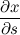 and and 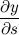 . .Substituting (2) into (1), we have: 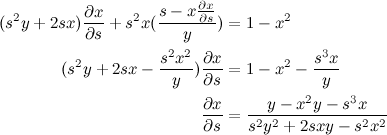 Substituting the above value of 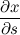 back into (2), we then obtain back into (2), we then obtain 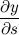 as: as: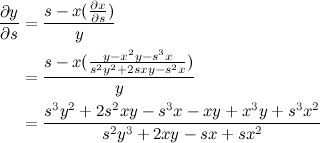 The end result is a little This post has been edited by v1n0d: Jan 3 2014, 07:57 PM |
|
|
 Jan 3 2014, 01:17 PM Jan 3 2014, 01:17 PM
Return to original view | Post
#37
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(RED-HAIR-SHANKS @ Jan 3 2014, 12:18 PM) I reckon it'll hit the acorn. When the archer aims horizontally and shoots an arrow straight at an acorn, the arrow will move slightly downwards in a curve due to some gravitational attraction towards the Earth. At the same time, the acorn will fall downwards too when Scrat drops the acorn. And if we ignore the air drag, the arrow will surely hit the acorn(assume that the acorn falls with an acceleration that is tantamount to the gravitational attraction, where a=g=9.8ms^-2). I too would like to know a bit more about this.This is just my estimation and bits of basic knowledge from my Physics SPM, I'd love to see some more detailed and explicit explanation. From what I recall in my physics classes (this was 10 years back OMG! Also, have fun at PLKN RED-HAIR-SHANKS, it's an amazing experience! This post has been edited by v1n0d: Jan 3 2014, 01:17 PM |
|
|
 Jan 3 2014, 04:54 PM Jan 3 2014, 04:54 PM
Return to original view | Post
#38
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(studyboy @ Jan 3 2014, 04:39 PM) Aren't both x and y functions of s? Good point. Looks like I've made a mistake. I've edited my previous post to reflect the corrected version.x=x(s), y=y(s)? How could you differentiate sxy and only treat one as a function of s? This post has been edited by v1n0d: Jan 3 2014, 08:00 PM |
|
|
 Jan 3 2014, 05:46 PM Jan 3 2014, 05:46 PM
Return to original view | Post
#39
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(Critical_Fallacy @ Jan 3 2014, 04:57 PM) Holy cow it's been ages since I've seen cycle notation! I have to be honest, all but forgotten how to multiply cycles. Will need to read up and refresh before I can answer your question. |
|
|
 Jan 3 2014, 06:27 PM Jan 3 2014, 06:27 PM
Return to original view | Post
#40
|
      
Senior Member
3,197 posts Joined: Mar 2007 From: Kuala Lumpur, Malaysia |
QUOTE(Critical_Fallacy @ Jan 3 2014, 05:58 PM) You're right, and there is a condition imposed by the initial velocity as mentioned by v1n0d. Thanks!If there were no gravity, the arrow would fly straight to Scrat and the acorn. Since gravity gives the dropped acorn and the released arrow the same constant acceleration downward, they each fall the same vertical distance below the positions they would have had with no gravity. Thus, the arrow ends up hitting the acorn no matter what the initial velocity** of the arrow. The higher the velocity of the arrow, the sooner they meet and the shorter the vertical distance that the acorn falls before being hit.  ** Assuming the arrow is fired from ground level, the initial velocity of the arrow must be higher than the minimum velocity given by: 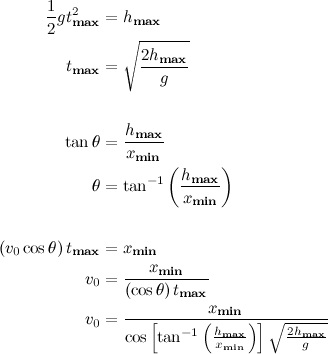 where hmax is the height of the acorn from ground before it is dropped, xmin is the horizontal distance of the archer away from Scrat / acorn, and tmax is the time of the acorn strikes the ground after it is released by Scrat. Regarding your previous question, is what does the operation o in SoD represent? I automatically assumed you were working on permutation cycles, but I can't get the same results as you. |
| Change to: |  0.3384sec 0.3384sec
 0.56 0.56
 7 queries 7 queries
 GZIP Disabled GZIP Disabled
Time is now: 19th December 2025 - 08:49 PM |