QUOTE(kingkingyyk @ Jan 3 2014, 08:16 PM)
Owh, that clarifies everything.

Here's another question, according to the lecturer :
Question 1 :
How many ways to arrange all alphabets in M A T H E M A T I C S such that the vowels are together.
Consonents : M T H M T C S => 7
Vowels : A E A I => 1
Answer = (7+1)! = 8!
Question 2 :
How many
different ways to arrange all alphabets in M A T H E M A T I C S such that the vowels are together.
Consonents : M T H M T C S => 7
Vowels : A E A I => 4
Answer = (8!/2!2!) x (4!/2!)
Do you know what is the difference?

I think they are the same (Question 1 answer should be same with Question 2 answer).

Let me try to explain this,
1) For this, the arrangement of the vowels do not matter. As long as they are together, be it AEAI, AAEI, IEAA or etc, they count as 1 entity. Hence the are 8! ways of arranging M A T H E M A T I C S.
2) For the second question, let us think of it via a 2 stage process.
STAGE i) The band of vowels can be rearrange so we have 4!. However, as mentioned by v1n0d, given the 2 As we have to divide 4! by 2! so there are in total 4!/2! ways of arranging the A A E I.
STAGE ii) Now, from Question 1 we know that we have 8! ways of arranging M A T H E M A T I C S so that the vowels are together. However, there are 2 M's and 2 T's so in effect, we have 8!/2!2! ways of doing the arrangement.
Therefore, according to the multiplication principal, we will have (8!/2!2!) x (4!/2!) ways of arrangement.
Nevertheless, I have absolutely no idea how the words used in Question 1 implies the answer given.

Let us wait what there others have to say about this.


 Jan 2 2014, 11:20 PM
Jan 2 2014, 11:20 PM

 Quote
Quote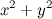 terms cancel out, which yields the following:
terms cancel out, which yields the following: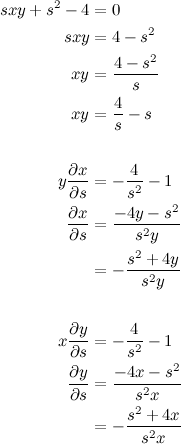

 0.0531sec
0.0531sec
 1.66
1.66
 7 queries
7 queries
 GZIP Disabled
GZIP Disabled