Based on hypotheses testing, I read from the notes and websites that if the p-value is lesser than the alpha value, the null hypothesis is rejected. Else, fail to reject.

However, I'm confused after I stumbled across this question. For a two-tailed question, the p-value lesser than the alpha value means that it falls inside the rejection region. But how does that make p-value < alpha value since based on the graph, it looks more logical that p-value > alpha value?






This post has been edited by UserU: Dec 7 2013, 02:21 AM

0.0275 is in critical region and shud reject null hypothesis

Indeed, but doesn't that make the p-value > critical value of 0.025, as shown in the first image?

Should be accepting null hypothesis. The answer is wrong I suppose

It should be. However, the majority of the answers this thread support the claim to reject, which don't make sense

So basically, the p-value will move towards the middle of the bell when its value increases?

I think you meant "do not reject null hypothesis"..

The question clearly stated that the p-value is 0.0275 resulted from a two-tailed t-test. This is clearly below 0.05 (5% significance).

So, reject the null hypothesis.

UserU observed the p-value (0.0275) is higher than the value 0.025 at one side. Shouldn't you should explain clearly to him about the 0.05 significance?

I think mumeichan does a better job in explaining this.

LOL. I'm a little busy at work right now, so before I come up with a long reply I'll need UserU to do a few things. He might just be able to figure it out himself.

Firstly, UserU is wrong in his conclusion but is thinking along the right path. So

1. Define what is a p-value
1a. Define p-value mathematically for a 1 tailed test
1b. Define p-value mathematically for a 2-tailed test
2. Define the alpha value in terms of the p-value.

If you still don't see it, I'll explain in the detail once I'm free.

P-value = Probability value that's used in hypothesis testing to determine the significance of an outcome

For both a and b, I don't understand as I have not learned about it mathematically yet.

Alpha value serves as the border between the level of significance(regions) and possibilities to produce a Type 1 error based on its value

Yeah! mumeichan is the Prince of Statistics in LYN!

Btw, thanks for the helpful replies. Waiting for the sifu to explain

P-values are actually the area under the extreme ends of the distribution (shown earlier).
Try to explain P-values relative to confidence intervals and perhaps do a simple sketch, and you will understand whats happening.

P-values can be easily explained/shown through the region cut-offs in both one-tail and two tail test.
Which I would call it more of a statistical explanation than mathematical (when one refers to mathematical, it usually includes uses of abstract mapping and functions, which is way beyond scope)

lastly the 0.05 rule is more of a convention based rule than reason based rule, dating back to problems in classical statistics.

First let me start by stating that the reason you cannot understand why you are wrong and the reason why the people in the other forum cannot explain their answer to you is because everyone doesn't know how to define p-values and alpha-values properly in layman language and mathematical notation.

It is not necessary for you to understand it if you just want to use statistics as a business tool just like a pilot doesn't need to understand completely the workings of an airplane to fly it. In practice he just needs to know what happens when he uses the controls.

Now back to your questions. Let's starts with a simple "continuous probability distribution function"



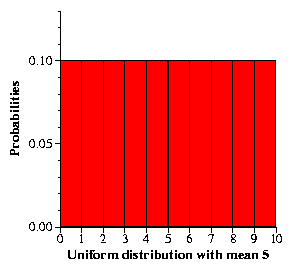
It's continuous in the sense any value between 0-10 is possible, ie. 5.6764567456.
If it was discrete, then only whole numbers 1,2,3,4 would be valid.

Now the probably of any exact value to occur is 0. That might seem counter-intuitive at first. But in statistic, a probability of 0 doesn't mean that the event cannot occur, it is just the lowest limit in the range of probabilities. The reasoning goes that there are really and infinite number of values between 0 and 10. You can write your decimals as long as you want. So to get a very exact values of say 4.454655762565 is very unlikely.

Hence a more practical way is to consider a 'range of events'. So we can say the the probability of getting more than 5 is 0.5 since the area between 5 and 10 covers 0.5 of the total area under the probability function line. So P(x>9) would be 0.1.

I hope this idea now comes intuitively to you. Now lets assume the graph above is the probability of closing stock prices tomorrow. And here is your situation. Your investment strategy will result in a loss if the price of the stock closes above 9 tomorrow. And you will only use this strategy if there is a 5% chance it will fail

So what would you do?

1. First see what is the probability of the price going above 9. Based on the graph it is .10
2. Determine is you are willing to take the risk. In this case no, since there is 10% chance of the price going above 9, hence a 10% chance of failure. But you already said you are only willing to take a 5% risk.

From the example above you can get a layman sense of p-values and alpha values.

Here 0.9 is the p-value for the an event/observation 9 or greater. Mathematically P(X>9)=0.1
And 0.05/5% is your alpha. Mathematically a=0.05

Graphically you can also see that 0.1 covers more area than your alpha.

We will come back to this later. Just keep all this in mind for now.

--------------------------------------------------------------------------------------------------------

Now lets put that example in hypothesis testings. That was an analog to 1-tail hypothesis test, since you only considered a case of values ranging out in one direction.

Typically hypothesis testing is used to determine the true statistic of the population when you only have data from a small sample. Say you're designing some stochastic model for a stock and you wanna determine if the probability of the price going up by 1 is 0.6. So you observe the stock for a month and you find that the price when up by 1 65% of the time. So in the long run, does the price of the stock really go up only 0.6 of the time?

Based on your standard deviation, you have determined that if the true probability is really 0.6, there is only a 1% chance that you will see a 0.65 probability or more this month you reject the null hypothesis of the prob being 0.6. Why did you reject it? Because sometime earlier you had arbitrarily decided that if you observed an event that only happens 5% of the time or rarer, you will reject it.

In this sense P(X>0.65)= P(0.65<x<1) = 0.01 (Probabilities are limited to 1)(Recall here I'm talking a probability of a probability. It could be a probability of a mean, or probability or a range or a probability of anything. I'm purposely making this more complicated because I think you can handle it as you're a CFA candidate)

---------------------------------------------------------------------------------------------------------------

Now lets go to a two-tail test. A two tail test looks are probability of values ranging to the right and left of your null hypothesis. In the example above, you will be testing for any value above or below 0.6.

So if you observed 0.65, you will have to consider P(X>0.65) given that the true value is is 0.6, in other words P(X>0.65|H0 is true). And since it's a two tail test P(X<.065|H0 is true) Just like above P(X>0.65|H0 is true)=0.01 and obviously P(X<0.65|H0 is true)=1-0.01=0.99. Since the observed value is above the null value, the statistic you're obviously interested in is P(X>0.65|H0 is true)=0.01

Now here is where your misunderstanding begins. The p-value is defined as 2*min{ P(X>observed|H0 is true) is true);P(X<observed|H0 is true)} = 2*{P(X>0.65|H0 is true)=0.01} = 0.02

--------------------------------------------------------------------------------------------------------------

Statisticians knew that statistics would most likely be used by people who did not understand statistics nor cared to. So the devised a simple rule.

If p-value is more than alpha, then fail to reject null
If p-value is less than alpha, then reject null

And it is normally the statisticians providing the p-values and the decision makers providing the alpha as the alpha is basically the amount of risk one is willing to take in being wrong. So it made things simpler to have the p-value multiplied than the alpha being halved.

Recap,

1-tail test:
Events to the right of null, pvalue = P(X>observed|H0 is true)
Events to the left of null, pvalue = P(X<observed|H0 is true)

2-tail test
pvalue = 2*min{ P(X>observed|H0 is true) is true);P(X<observed|H0 is true)}

It doesn't matter what probability distributions you use. It can be normal or whatnot. The concept is the same.

A good explanation.

Back to UserU's question, is there a need to multiply the given p-value by 2 before comparing it with the 5% significance?

No because in the question, the 'p-value' and not the actual probability statement was given.

This has practical importance because say his future company uses SPSS or SAS, the generated report of the two tailed t-test is gonna give the p-value and not the actualy probability.

Thank you

Hi mumeichan, thank you for the explanation, but I still have some doubts. I'm not a CFA candidate, just a student taking up Introduction to Statistics so go easy on me.

First, you mentioned that the probability of 0 doesn't mean its impossible. Are you implying that values such as 0.0001 or <0.001 are still rounded off as zero? An example here interprets the probability of zero as an impossible event; not studying maths in school.

Second, based on your reply to Blofeld's question:
Say, I've used SAS for lab exercises but if I'm answering questions in an exam, I would still have to double the p-value for two-tailed tests? From the attachment below, I can also use either p-value*2 against 0.05 or p-value against 0.025?

Misconceptions about p-value ::

(1) p-value ≠ 1 - Φ(|z|)

(2) p^-value ≠ 2 × (p-value)

p-value made EASY!
*****************


For a two-tailed z test, p-value is calculated as

p-value = 2*P(Z>|z|)

Φ(z) = P(Z ≤ z)

where Φ is the Cumulative Distribution Function for the normal distribution

P(Z>|z|) = 1 − P(Z ≤ z) = 1 − Φ(|z|)

p-value = 2*[1 - Φ(|z|)]

1. For a continuous distribution, there are an infinite number of possible-event/values within a range. Hence a probability is defined as the integral of f(x) from a to b, with f(x) being your probability density function.

So you might ask what is the probability of one point, say 'a'? a could be 3.35246 for example.

We apply the definition, which in integral from a to a of f(x). What is that? It is F(a)+C -F(a) +C = 0. If you look at it, as b approaches a from the right, the integral from a to b gets closer and closer to 0.

Another way is to use another definition of probability which is (number of outcomes of interest)/(total number of possible outcomes)

You will get 1/infinity, which you can analyze by doing 1/b as b->inf. You will see that it approaches 0.

Now while the probability is 0, it is not that 3.35246 is not a possible event, it's just very unlikely you will pick that exact number in a random selection.

An impossible event will have a probability of 0, but a probability of 0 does not imply an impossible event.

Same goes with a probability of 1. It doesn't mean it will happen definitely. Let's prove it.

What is the probability of NOT selecting 3.35246? It will be 1-Pr(selecting 3.35246). Which is 1-0=1

But we do know it is possible to select 3.35246, thus even though the probability is 1, it's not guaranteed.

Like all statistical construct, the meaning and value of any 'statistic' merely rest upon it's definition and intended usage.

2. I hope you really read my long explanation.

p-value is NOT the probability of an event. p-value is what what you use to compare against the alpha value.

When you look up your normal/z-score table, please read everything on the page and see that it is defined as P(Z<z). Same goes with the question, see if they are giving you the p-value or the probability in the form of P(X<some number)

This post has been edited by mumeichan: Dec 10 2013, 11:15 PM