Outline ·
[ Standard ] ·
Linear+
WTA about maths, forming an equation
|
TS~~SkyShuT_T3r~~
|
 Apr 13 2011, 09:35 PM, updated 15y ago Apr 13 2011, 09:35 PM, updated 15y ago
|
Getting Started
 

|
So here's the question: The cost of fuel to propel a boat through the water (in dollars per hour) is proportional to the cube of the speed. A certain ferry boat uses $100 worth of fuel per hour when cruising at 10 miles per hour. Apart from the fuel, the cost of running this ferry (labour, maintenance, and so on) is $675 per hour. At what speed should it travel so as to minimise the cost per mile traveled? The graph should be somewhat like this i think, 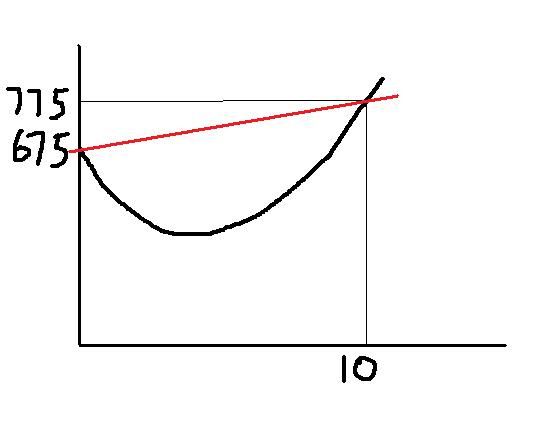 but problem is I can only find the equation for the red line from the information given, how can I find the equation for the curve? In need to be enlightened.  |
|
|
|
|
|
dkk
|
 Apr 13 2011, 10:40 PM Apr 13 2011, 10:40 PM
|
10k Club


|
fuelcost per hour = speed ^ 3 * k => $100 = 10^3 * k => k = 100 / 1000 = 0.1 therefore fuelcost per hour = speed ^ 3 * 0.1 labourcost per hour = 675 to get cost per mile, divide cost per hour by speed fuelcost per mile = speed ^ 3 * 0.1 / speed = speed ^ 2 * 0.1 labourcost per mile = 675 / speed let x be speed plug this into the graphing program at http://rechneronline.de/function-graphs/load&save settings: a0=2&a1=x*x*0.1+675/x&a2=x^2*0.1&a3=675/x&a4=1&a5=4&a6=8&a7=1&a8=1&a9=1&b0=500&b1=500&b2=-10&b3=50&b4=-10&b5=300&b6=10&b7=10&b8=5&b9=5&c0=3&c1=0&c2=1&c3=1&c4=1&c5=1&c6=1&c7=0&c8=0&c9=0&d0=1&d1=20&d2=20&d3=0&d4=&d5=&d6=&d7=&d8=&d9=&e0=&e1=&e2=&e3=&e4=14&e5=14&e6=13&e7=12&e8=0&e9=0&f0=0&f1=1&f2=1&f3=0&f4=0&f5=&f6=&f7=&f8=&f9=&g0=&g1=1&g2=1&g3=0&g4=0&g5=0&g6=Y&g7=ffffff&g8=a0b0c0&g9=6080a0&h0=1&z[attachmentid=2154542][attachmentid=2154542] This post has been edited by dkk: Apr 13 2011, 10:42 PM Attached thumbnail(s)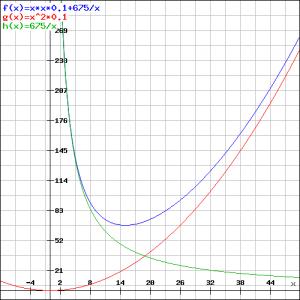
|
|
|
|
|



 Apr 13 2011, 09:35 PM, updated 15y ago
Apr 13 2011, 09:35 PM, updated 15y ago
 Quote
Quote
 0.0157sec
0.0157sec
 0.94
0.94
 6 queries
6 queries
 GZIP Disabled
GZIP Disabled